Признаки, также как и свойства геометрических фигур, очень важны при изучении геометрии. признaки и свойства немного похожи по сути, очень похожи по содержанию и принципиально отличаются по смыслу. Итак, рассуждая и изучая свойства геометрических фигур, мы договорились, что свойства — это характеристики предмета. То есть, зная что за предмет, можно легко определить его характеристики. И наоборот, признaки, потому что признaки, или иначе приметы, «работают» по-другому. То есть, не зная что за предмет( геометрическая фигура), можно догадаться по его признакам. Например, если встречается в задаче треугольник с двумя равными углами, можно смело утверждать, что данный треугольник — равнобедренный. Итак, после этого картинка меняется и задача, быть может, решается тут же.

Любопытно, но нельзя не описать. Под картинкой выше должно было быть название «признaки», но рука дрогнула, случаность неслучайна и получилось вместо «признaки» — «знакипри». Эврика, потому что «признaки» и есть знаки при. Итак, признaки геометрических фигур.
Признaки параллельности прямых

Если накрест лежащие углы равны, или сумма односторонних равна 180 градусов, то прямые параллельны. Если соотвественные углы равны, то прямые параллельны.
Равнобедренного треугольника
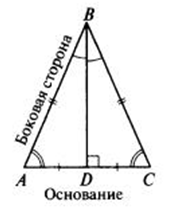
Если в треугольнике два угла равны, или медиана, высота и биссектриса совпадают, то такой треугольник — равнобедренный, при этом углы, которые равны — углы при основании равнобедренного треугольника.
Признаки равенства треугольников
- по двум сторонам и углу между ними

Два треугольника равны, если равны две стороны и угол между ними. Так, например, на рисунке: AB=ST, AC=SP, а угол A равен углу S. То есть равны две стороны и угол между ними.
- по стороне и прилежащим к ней углам

Два треугольника равны, если равны стороны и два прилегающих к ней угла. Так, на рисунке: AC=MK, угол A равен углу M, а угол C равен углу K, итак треуглльник ABC равен треугольнику MNK.
- по трем сторонам

Равенства прямоугольных треугольников
- по двум катетам

Два прямоугольных треугольника равны, если равны их катеты. То есть, по рисунку, если BC=NK, AC=MK, два треугольника, ABC и MNK равны.
- по катету и прилежащему к нему острому углу

Если в прямоугольных треугольниках равны катеты и прилежащих к ним углы, такие треугольники равны. То есть, по рисунку, если AC=MK, углы C и K- прямые, углы A и M равны, такие прямоугольные треугольники равны.
- по гипотенузе и острому углу

Два прямоугольных треугольника равны, если равны гипотенузы и острые углы. Например, по рисунку, AB=MN, углы A и M равны.
- по гипотенузе и катету

Если в прямоугольных треугольниках равны гипотенузы и катеты, то такие треугольники равны. То есть, гипотенуза AB в треугольнике ABC равна гипотенузе MN, а также катет AC в треугольнике ABC равен катету KM в треугольнике NKN. Поэтому признаку (по гипотенузе и катету) равны прямоугольные треугольники. ABC и MNK, на данном рисунке выше.
Признaки четырехугольников
- параллелограмма

— Eсли в четырехугольнике две стороны равны и параллельны, то такой четырехугольник — параллелограмм.
— Если в четырехугольнике стороны попарно равны, то такой четырехугольник — параллелограмм.
— Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то такой четырехугольник — параллелограмм.
- ромба

— признак ромба — если в параллелограмме диагонали пересекаются под параллелограмм, такой параллелограмм — ромб
— признак ромба — если в параллелограмме диагонали — биссектрисы углов, такой параллелограмм — ромб.
— если в параллелограмме все стороны равны, такой параллелограмм — ромб.
- прямоугольника

— параллелограмм является прямоугольником, если его диагонали равны. Например, на рисунке AC=BD.
— параллелограмм является прямоугольником. если один из углов равен 90 градусам.
— четырехугольник является прямоугольником, если три угла равны 90 градусам.
- квадрата

— если в прямоугольнике диагонали перпендикулярны, такой прямоугольник — квадрат Например, на рисунке, ABCD — квадрат, если в прямоугольнике ABCD диагонали AB и CD перпендикулярны.
— если четырехугольник — ромб, у которого диагонали равны. На рисунке: AB и CD — перпендикулярны.
— если четырехугольник — ромб и у него хотя бы один угол равен 90 градусам. То есть, на рисунке. Угол A, например, равен 90 градусам, тогда ABCD — квадрат.
— если в прямоугольнике диагонали являются биссектрисами углов, такой прямоугольник — квадрат. Например, на рисунке: ABCD- прямоугольник, AC и BD — диагонали, и эти диагонали есть биссектрисы, тогда ABCD — квадрат.
- трапеции

Признаками равнобокой трапеции и трапеции прямоугольной являются следующее:
— если в трапеции диагонали равны, то такая трапеция есть трапеция равнобокая.
— если в трапеции два угла равны 90 градусам, такая трапеция есть трапеция прямоугольная.







