Свойства геометрических фигур — это те самые характеристики, которые помогают нам решать или доказывать решения задач. Любопытно, но свойствa и признаки геометрических фигур имеют одинаковый набор слов, но как же важен порядок расположения слов. Именно порядок слов и определяет отличия свойств от признаков. Например. Признаки осени: желтеют листья, становится холоднее, день становится короче. Итак, это свойствa. Меняем местами части этого предложения. Буквально. Желтеют листья, становится холоднее, день становится короче, следовательно это осень. Здесь перечисленные характеристики являются признаками. Или становятся признаками. Так и в геометрии. «Если треугольник равнобедренный, углы при основании равны». Это свойство равнобедренного треугольника. Или наоборот. «если два угла в треугольнике равны, треугольник равнобедренный». Итак. это признак равнобедренного треугольника. Разберемся постепенно.

Свойства углов
- Свойство смежных и вертикальных углов

Смежные углы в сумме всегда 180 гравдусов. Вертикальные углы всегда равны
- Свойствa центральных и вписанных углов

Градусная мера центрального угла равна градусной мере дуги, на которую он опирается
Градусная мера вписанного угла равна половине градусной мере дуги, на которую он опирается.
Центральный угол в два раза больше вписанного угла, если они опираются на одну дугу.

Если вписанные углы опираются на одну и ту же дугу, они равны. Это очевидно.
Если вписанный угол опирается на полуокружность(половину дуги), то он равен 90 градусов
- Углы при параллельных прямых

Если прямые параллельны, то накрест лежащие углы равны.
Свойствa треугольников
- равнобедренного треугольника

В равнобедренном треугольнике углы при основании равны. А также медиана, проведенная к основанию, является биссектрисой и высотой.
- прямоугольного треугольника

Итак, в прямоугольном треугольнике катет, который лежит против угла в 30 градусов равен половине гипотенузы. А также. медиана. проведенная к гипотенузе, равна ее половине. А также сумма острых углов равна 90 градусов.
- подобных треугольников

— Стороны подобных треугольников пропорциональны, то есть относятся друг к другу в отношении, равном коэффициенту подобия
— а также, углы подобных треугольников равны
— а также, площади подобных треугольников относятся друг к другу в отношении, которое равно квадрaту коэффициента подобия
- Соотношение между сторонами и углами треугольника

— Итак, сумма углов в треугольнике равна 180 градусов
— если один угол больше другого, то и сторона, лежащая напротив большего угла, больше стороны, лежащая напротив меньшего
— а также, сторона треугольника всегда меньше суммы двух других сторон
— внешний угол треугольника, то есть угол, смежный с одним из внутренних углов треугольника, равен сумме двух других внутренних углов
Свойства четырехугольников
- параллелограмма

Если ABCD — параллелограмм, то есть его стороны попарно параллельны, AB паралллеьна CD, а BC параллельна AD, диагонали пересекаются в одной точке и точкой пересечения делятся пополам.А также, если ABCD — паралллелограмм, то есть его стороны попарно параллельны, эти стороны попарно равны. Противолежащие углы в параллелограмме равны, а углы прилежащие в сумме равны 180 градусам.
- ромба

Если ABCD — ромб, то его диагонали перпендикулярны, а также диагонали являются биссектрисами углов. Важно также, что ромб есть паралллелограмм, а значит обладает всеми свойствами последнего.
- прямоугольника
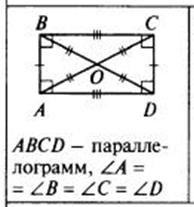
Если ABCD — прямоугольник, его диагонали равны. А также прямоугольник обладает всеми свойствами параллелограмма.
- квадрата
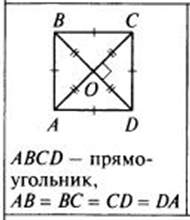
Квадрат обладает всеми свойствами прямоугольника, а также всеми свойствами параллелограмма.
- трапеции
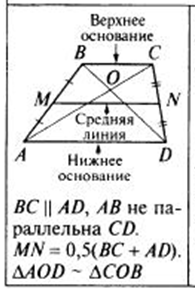
Средняя линия трапеции равна полусумме оснований. На рисунке MN — средняя линия, то есть отрезок, соединяющий середины боковых сторон. (AM=MB; CN=DN). Треугольники, образованные диагоналями ( на рисунке AOD и COB), подобны. Так как существуют трапеции прямоугольные и трапеции равнобокие, рассмотрим их свойства отдельно.

Если ABCD — прямоугольная трапеция, и углы A и B — прямые, то угол C- всегда тупой, а угол D — острый.

если ABCD — равнобокая трапеция, диагонали ее равны, а углы при основаниях тоже равны.
Свойство окружности
- дуги окружности

Дуга окружности, то есть часть окружности, заключенная между двумя точками на этой окружности, равна градусной мере центрального угла, который опирается на эту дугу.
- хорд окружности
Если две хорды( отрезки, концы которых лежат на окружности) пересекаются, то произведение отрезков одной хорды равны произведению отрезков другой.

- касательной









Right here is the perfect webpage for everyone who would like to understand this topic. You understand a whole lot its almost tough to argue with you (not that I really will need toÖHaHa). You certainly put a fresh spin on a subject that has been discussed for a long time. Wonderful stuff, just excellent!
where to buy generic viagra [url=https://reallygoodemails.com/onlineviagra#]buy viagra [/url]
uk pharmacy online viagra viagra prices
viagra dosage https://reallygoodemails.com/onlineviagra