Все определения геометрии собраны вместе в этой статье. Прежде, чем разбирать и систематизировать все теоремы и формулы. Прежде необходимо пределиться со всеми основными принципами. Определиться с определения ми. Итак.
Углы.Основные определения
- Углы смежные и вертикальные.

Итак, ∠DBC и ∠DBA на рисунке слева, это смежные углы. Определения. Итак, у них общая вершина и одна общая сторона, две другие продолжают друг друга и образуют прямую линию. Вертикальные углы (AOC и DOB) на рисунке справа. Так как вертикальные углы образуются при пересечении двух прямых. Важно. Смежные углы и углы вертикальные всегда «работают» в паре. И обладают рядом замечательных свойств, но об этом позже и в отдельной статье.
- Накрест лежащие, односторонние, соответственные углы

Определение: при пересечении двух параллельных прямых третьей прямой образуются пары углов, а третья прямая называется секущей. Итак, с углами попробуем разобраться. Углов получается невероятно много, но, разберем позже, отдельно, в статье про свойства, градусных мер всего две. Итак.
Накрест лежащие углы — 3 и 6, 4 и 5
Односторонние углы — 3 и 5, 4 и 6
Соответственные углы — 5 и 2, 7 и 3, 6 и 1, 8 и 4
Треугольники.
- Остроугольные. Тупоугольные. Прямоугольные

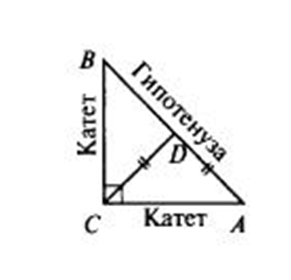
Определения. В остроугольных треугольниках все углы острые, а в тупоугольных — угол (только один) — тупой. Итак, в прямоугольном треугольнике один угол прямой, при этом две стороны называются катетами, а третья сторона называется гипотенузой.
- Равнобедренные. Равносторонние
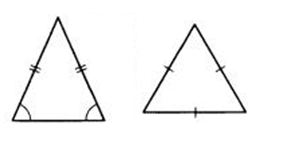
Итак, равнобедренные треугольники — это треугольники, у которых две стороны равны, при этом стороны называются боковыми, а третья сторона называются основанием.

- Равные треугольники
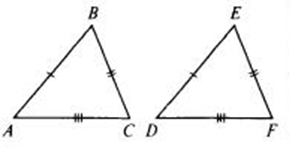
Равные треугольники — треугольники, у которых равны все соответствующие элементы, то есть равны углы, равны стороны. Итак, по рисунку AB=DE, BC=EF, AC=DF.
- Подобные треугольники

Треугольники подобные, если равны соответсвующие углы, а сходственные (соответствующие) стороны пропорциональны. Коэффициент пропорциональности называется коэффициентом подобия и обозначается, как правило, буквой k.

- Средняя лииния треугольника
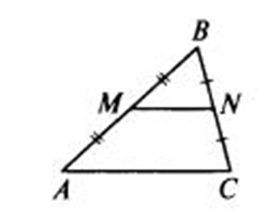
Итак, это отрезок, соединяющий середины противоположных сторон, всего их три.
- Медиана. Биссектриса. Высота.

Итак, медиана — это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Итак, биссектриса — это луч, который делит угол пополам.
Перпендикуляр, который опущен из вершины треугольника на противолежащую сторону, называется высотой, и важно: всего в треугольнике три медианы, три высоты и три биссектрисы, так как три вершины.

ТРЕУГОЛЬНИКИ
Четырехугольники.Основные определения
- Параллелограмм
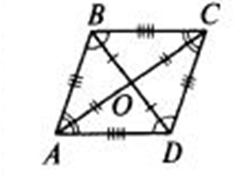
Если в четырехугольнике стороны попарно параллельны, он называется параллелограммом.
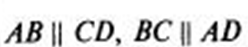
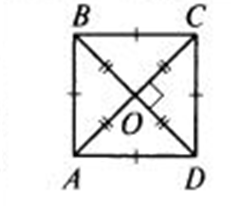
- Ромб

итак, четырехугольник, у которого стороны равны, называется ромбом.
- Прямоугольник
Это параллелогрaмм, у которого все углы прямые
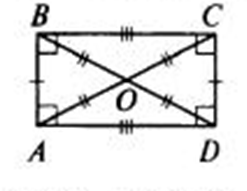
- Квадрaт
Итак,квадрат — это прямоугольник, у которого стороны равны
- Трапеция
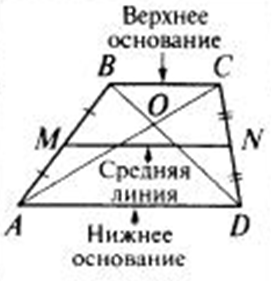
Итак, четырехугольник, у которого две стороны параллельны, называется трапецией, при этом они называются основаниями, а две другие строго нет, при этом параллельные стороны называются основаниями, две другие — боковыми сторонами. Трапеции бывают равнобокие и прямоугольные, называются так потому, что в равнобоких трапециях боковые стороны равны. в прямоугольной трапеции угол при основнии прямой (боковая сторона перпендикулярна основанию).








Right here is the perfect webpage for everyone who would like to understand this topic. You understand a whole lot its almost tough to argue with you (not that I really will need toÖHaHa). You certainly put a fresh spin on a subject that has been discussed for a long time. Wonderful stuff, just excellent!
This design is incredible! You obviously know how to keep a
reader entertained. Between your wit and your videos, I was almost moved
to start my own blog (well, almost…HaHa!) Great job.
I really enjoyed what you had to say, and more
than that, how you presented it. Too cool!