Текстовые задачиОГЭ — это самое нелюбимое и самое трудное, а текстовые задачи ОГЭ на совместную работу — нелюбимое и страшное вдвойне! Задачи такого типа чаще других заданий попадают в зону «трудных» заданий.
Текстoвые задачи на совместную работу. Работа -не волк.
Чтобы легко решать задачи вообще, а именно задачи про работу, нужно разобраться. А нужна ли работа? Что такое работа? Ведь чаще всего под работой понимают объем выполненной работы. Не работа как таковая, а результат.
Задачи на работу сильно напоминают по сути задачи про движение, потому что формула одна и формула очень похожа на основную формулу на нахождение пути, вспомним:
S = v• t, где S- путь, v –скорость, t –время.
Текстовые задачи на совместную работу. На примерах.
Итак, чтобы найти объем проделанной работы, нужно умножить объем работы, выполненной за час, на количество часов. Очевидно. По сути суть одна, поэтому введем понятие.
Производительность
это объем работы, которую выполнили за час.

Иначе производительность можно назвать скоростью, то есть скоростью выполнения работы. Итак, на примере.
- Задача 1. Тип 1.
На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
Решение будет алгебраическим, так как два неизвестных, то есть два неизвестных известным способом связанных между собой.
Итак, пусть x – производительность ученика,то есть столько деталей делает ученик в час, а (x+4)- столько деталей делает мастер в час, тогда

Но теперь составим уравнение. Так как ученик тратит на 11 часов больше, чем мастер, конструкция будет такой:
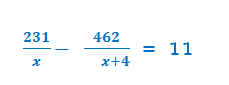
Решая уравнение( решение не приводится, так как решение типичное, получаем: x = -28; 3.
Итак, получаем ответ: ученик делает 3 детали в час(естественно, отрицательный ответ нам не годится).
- Задача 2. Тип 2.
Задачи на совместную работу бывают не только про учеников и мастера. Часто важным персонажем этих детективных историй становится бассейн. «Плавать раньше, чем ходить» или «Внимание, трубы».

Действие обычно происходит так: две трубы наполняют бассейн, затем этот же бассейн напоняет одна труба, потом вторая, а также наоборот. Но наша задача — считать за какое время наполнит одна, вторая, обе или как-то иначе, потому что все зависит от сценария. Итак, пример.
Примеры задач на совместную работу.
Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объёмом 136 литров?
Решение.
Пусть x – литров воды в минуту пропускает вторая труба, тогда x-2 – первая.
Найдем время работы этих труб

Составляем уравнение:
Так как вторая труба на 4 минуты быстрее,
ПОЛУЧАЕМ:

Решение оставляем за кадром, получаем корни
x = 10; -6,5
Очевидно, корень уравнения x = -6,5 не жизнеспособен, остаемся с x= 10. Задача решена. Все просто.
- Задача 3. Тип 3

Нетипично. Непривычно. Встречается в ЕГЭ. ВАЖНО.
Если объем работы не задан.
Если объем работы не задан, берем его за 1
Вспоминая аналогию с задачами на движение, обозначим скорости мальчиков (их производительность) как v1; v2; v3 (производительности Игоря, Паши и Володи),
тогда время работы соответственно равно;
Это время каждого мальчика в отдельности. По условию задачи мальчики работали «в паре»
Поэтому получаем:

Преобразуем и получим систему:
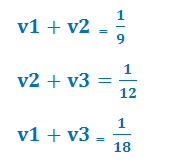
Эта оригинальная система решается оригинально
Сложим все уравнения системы:


С легким паром!








Right here is the perfect webpage for everyone who would like to understand this topic. You understand a whole lot its almost tough to argue with you (not that I really will need toÖHaHa). You certainly put a fresh spin on a subject that has been discussed for a long time. Wonderful stuff, just excellent!