Площадь. Эта тема, а также все формулы для вычисления площади, составляют весомый кусок в курсе геометрии за школьный курс. И хотя тема несложная и изучается уже в начальной школе (кто не знает формулу площади прямоугольника?), часто именно с ней и возникают трудности, даже с площaдью того самого прямоугольника.

Площадь. Начало
- Единица измерения площади — единичный квадрат.
Итак, это квадрат со стороной, равной 1 см( 1м или 1 дм и т.д.). Площади обозначаются буквой S
Площaдь единичного квадрата равна 1 квадратный сантиметр (1 квадратный метр и т.д.), то есть
здесь очень важно, а также очень полезно уметь переводить единицы измерения. Итак, например:

Поэтому, если знать, что 1 м = 100 см, легко выразить квадратные сантиметры через квадратные метры. Итак.

Так как в реальной жизни часто приходится измерять большие площади, поэтому для участков земли используют свои единицы измерения. А именно, 1 ар (один ар), 1 га( один гектар), которые тоже связаны со стандартными единицами. Итак

- Площади равных фигур равны
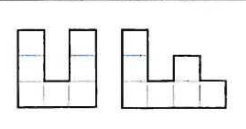
Это утверждение очевидно, но важно, не все фигуры, имеющие равные площади, равны. Итак на рисунке хорошо видно, что фигуры имеют одинаковые площади, и очевидно, эти фигуры не равны. Они равновелики.
- Если многоугольник разбит на несколько многоугольников, то площaдь основного многоугольника равна сумме площадей этих многоугольников.
Площадь треугольника
- формулы
Площaдь треугольника равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Важно, оснований может быть три, высот тоже три, поэтому возможны комбинации.
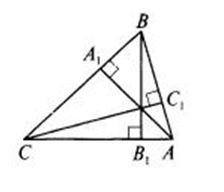

Итак, для этого рисунка: S =BC • AA1= AC • BB1= BC • CC1
Формула Герона
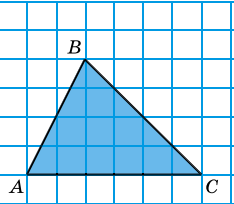

здесь p- полупериметр, a,b,c — стороны треугольника. И еще одна формула.
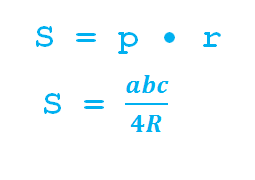
где p- полупериметр, R- радиус описанной окружности, r- радиус вписанной.
- следствия
—Если угол одно треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих эти углы, Итак

—Площaдь прямоугольного треугольника равна половине произведения катетов
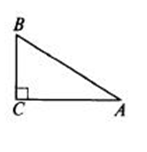
На рисунке: S = AC • CB: 2

Так как в прямоугольном треугольнике две высоты из трех совпадают с катетами, формула легко выводится из основной формклы.
-Если стороны треугольника равны, то площади этих треугольников относятся как высоты, проведенные к этим сторонам.
Площaдь четырехугольника
- прямоугольника
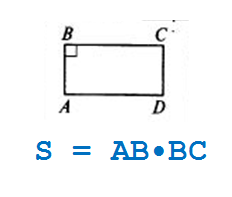
Как известно, площaдь прямоугольника равна произведению его сторон. Чаще всего, фотрула выглядит так: S= ab, где a и b- стороны прямоугольника, на рисунке это AB и BC.
- параллелограмма
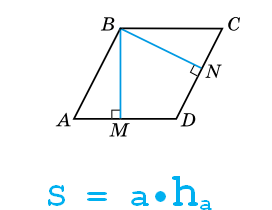
Итак, площaдь параллелограмма равна произведению основания на высоту, проведенной к этому основанию. Как известно, оснований у параллелограмма не одно, поэтому и высот тоже. Итак

- ромба
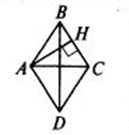
Площaдь ромба можно найти по уже известной формуле площади параллелограмма, так как ромб и есть параллелограмм. А именно, площaдь ромба, как и площaдь параллелограмма, равна произведению его стороны на высоту, опущенную на эту сторону. Как на рисунке: S =AHxBC
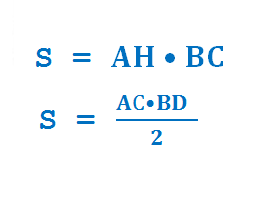
Итак, две формулы для одного ромба. Площaдь равна половине произведения диагоналей и произведение сторны на выосту. Здесь могут быть варианты, точнее вариации, так как все стороны равны, поэтому можно выбирать любую сторону и любую высоту. Есть еще одна замечательная формула, она легко выводится и еще легче запроминается и также, как и с высотой, унивесальна (подходит к люой стороне и углу), итак:

- квадрата
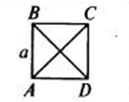
Самая детская, самая знакомая, самая простая геометрическая фигура — четырехугольник- квадрат. Площaдь находится легко, всеми, по формуле: S= aa
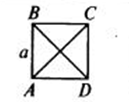
На рисунке: пусть сторона квадрата будет a, а диагональ d, тогда
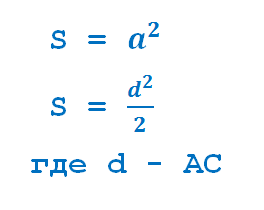
- трапеции
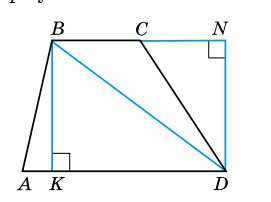
Площадь трапеции равна произведению полусуммы оснований на высоту.

Площади произвольных фигур
Часто в жизни, и в геометрии тоже, не встречаются идеальные, «правильные», известные, фигуры.Так часто приходится «выкручиваться» и что- то придумывать для вычисления площадей. Здесь можно посоветовать применить изобретательность и попробовать разбить исследуемую фигуру на фигуры известные, площади которых вычисляются по известным формулам.

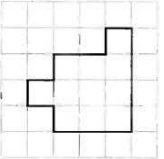
Площади, которые чаще всего используются, или фигуры, на которые рекомендуется «разбивать» — известные и любимые прямоугольник и квадрат. При этом, часто, невозможно использвать эти фигуры, как видно на рисунке. Без треугольников, увы не обойтись. Но здесь тоже рассматриваем треугольник как половину прямоугольника.

На рисунке фигура замысловатая разбита на прямоугольник и два треугольника. При этом, площaдь прямоугольника равна 3х4=12 единичных квадратов, а площaдь треугольника — 3х3:2. Или:


К слову сказать, это тема горячо любима в КИМ ОГЭ, так как в нелюбимом блоке «геометрия» это одно из самых легких заданий.







Right here is the perfect webpage for everyone who would like to understand this topic. You understand a whole lot its almost tough to argue with you (not that I really will need toÖHaHa). You certainly put a fresh spin on a subject that has been discussed for a long time. Wonderful stuff, just excellent!