Все теоремы геометрии, а точнее, вся теория геометрии, но с одной оговоркой, потому что здесь сключительно теория геометрии школьного курса. Не любима и не понимаема геометрия исключительно потому, что до конца непонятны и, соответственно, не приняты правила игры, поэтому сложно, а из-за этого часто невозможно выучить ценнейшую информацию из учебников. Учебники переписываются, усовершенствуются, очевидно, или тогда зачем? Но теория в учебниках становится все страшнее и страшнее, а потому непонятнее и непонятнее. Чтобы теорема стала любимым и понятным инструментом, чтобы теорема нужная всегда была «под рукой», все они собраны здесь.

ТЕОРЕМА О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА
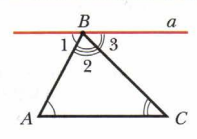
Сумма углов в треугольнике равна 180 градусов. Рисунок здесь не случайно, так как легко доказать, хорошо видно, что сумма углов равна 180, если провести прямую a так, чтобы прямые AC и a были параллельны. Из этой теоремы выходят замечательные следствия, а именно
- среди углов треугольника точно два острые, потому что, если угол тупой имеет градусную меру больше, чем 90 градусов. То есть сумма двух углов будет больше 180, но это невозможно, так как сумма углов в треугольнике равна 180 (см выше).
- Итак, Bнешний угoл треугольника равен сумме углов, не смежных с ним. (Внешний угoл треугольника — это угол, смежный с внутренним углом). Итак, сумма углов в треугольнике равна 180 градусов, поэтому сумма углов 1,2 и 3 равна 180. Но сумма углов 3 и 4 также равна 180, потому что углы 3 и 4 — смежные. Итак, угло 4 и равен сумме углов 1 и 2.
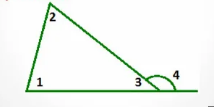
- внeшний угол треугольника больше каждого из углов треугольника, не смежных с ним), так как из выше доказанного следует, что угол 4 точно больше одного из углов 1 или 2, так как равен их сумме
- сторона треугольника меньше суммы двух других сторон (неравенство треугольника)
- в треугольнике против большего угла лежит большая сторона и наоборот, против большего угла лежит большая сторона.
ТEОРЕМА О СРЕДНЕЙ ЛИНИИ ТРЕУГОЛЬНИКА
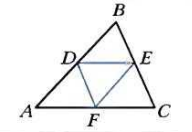
Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
Очевидно, что в каждом треугольнике может быть три средние линии, потому что можно построить отрезок, параллельный стороне, и построить трижды, при этом периметр треугольника, образованного этими линиями, в два раза меньше периметра основного треугольника. Эта теорема легко доказывается.
ТЕОРЕМА О СРЕДНЕЙ ЛИНИИ ТРАПЕЦИИ

Средняя линия трапеции параллельна основаниям и равна их полусумме.
Итак, на рисунке: BC, AD — основания, MN — средняя линия трапеции ( отрезок, соединяющий середины боковых сторон), MN=( BC + AD)/2

Итак, формула для нахождения средней линии трапеции легко выводится, для этогона рисунке выше указаны все необходимые дополнительные построения.
ТЕОРЕМА ПИФАГОРА
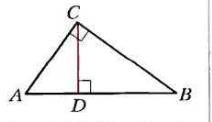
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
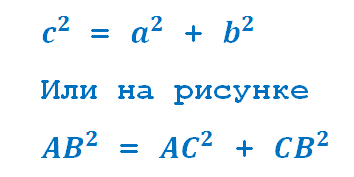
ТEОРЕМА ФАЛЕСА
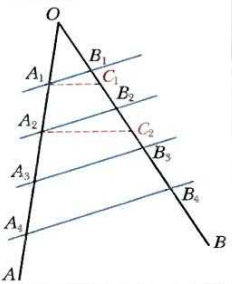
Если две параллельные прямые, пересекающие стороны угла, отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой.
ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ
Отношение двух отрезков—
отношение их длин, выраженных в одних и тех же единицах измерения
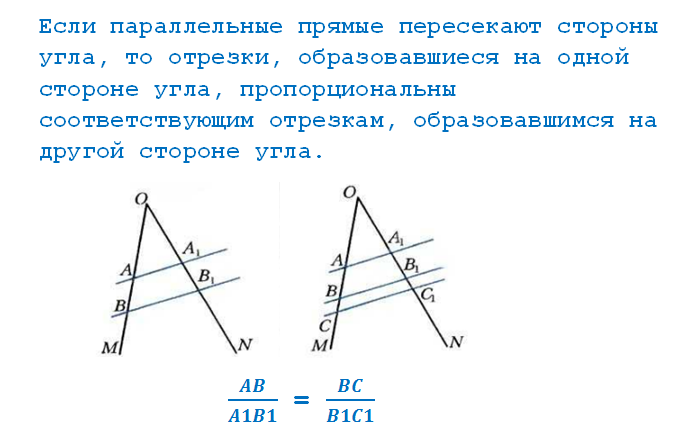
Но важно, что эта теорема справедлива и для любых двух прямых, которые взяли вместо сторон угла.
ТЕОРЕМА О МЕДИАНЕ И БИССЕКТРИСЕ ТРЕУГОЛЬНИКА
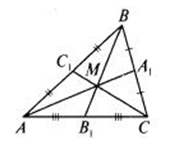
Три медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины треугольника. Итак, на рисунке:
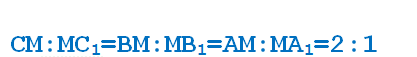

Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим к ним сторонам. То есть на рисунке:
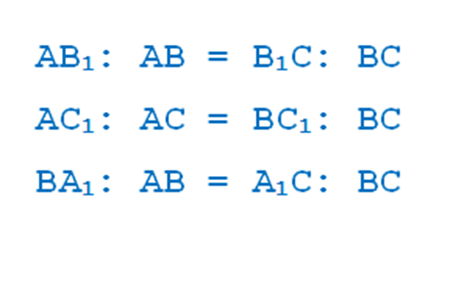
ТЕОРЕМА МЕНЕЛАЯ
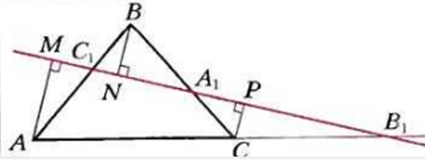
Итак, точки, лежащие на одной прямой, называются коллинеарными. То есть две точки всегда коллинеарны. Итак, условие коллинеарности трех точек:

Итак, три точки коллинеарны, если выполняются условия:

ТEОРЕМА ЧЕВЫ
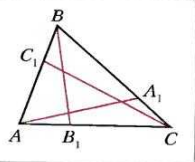
Если ABC — треугольник, A1, A2, A3— произвольные точки. AA1, BB1, CC1 — чевианы трегольника ABC, итак. Если чевианы являются биссектрисами, медианами или высотами, то они пересекаются в одной точке. Если прямые пересекаются в одной точке, они называются конкурентными. Итак, критерий конкурентности произвольных трех чевиан
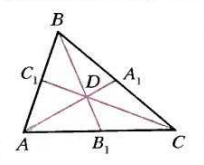
Для того, чтобы чевианы AA1, BB1, CC1 треугольника ABC пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство

ТЕOРЕМА ПТОЛЕМЕЯ
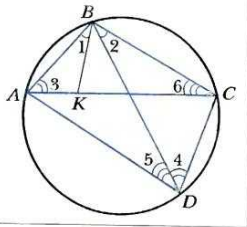
Произведение диагоналей вписанного в окружность четырехугольника равно сум ме произведений его противолежащих сторон. Итак,

ТЕОРEМА СИНУСОВ
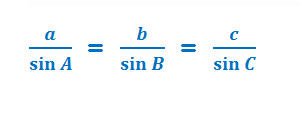
Стороны треугольников пропорциональны синусам противолежащих углов.
А также, для любого треугольника справедливо следующее:
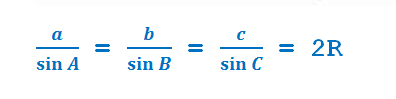
где R — радиус описанной окружности. Итак, отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.
ТЕОРЕМА КОСИНУСОВ
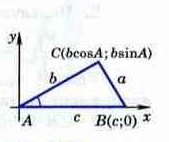
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними

Теоремa косинусов есть обощенная теоремa Пифагора, так как косинус прямого угла равен 0. Итак
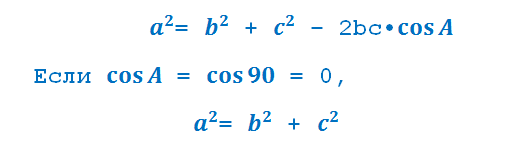
Это, конечно не все теоремы геометрии. И даже не все теоремы школьного курса геометрии. но точно все самые популярные, самые нужные и самые понятные. Всем нам больших успехов!!!








