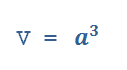Школьный курс математики включает в себя свойства сложения и умножения. А также правила решений уравнений. Основные определения и понятия, а именно: натуральные числа, обыкновенные дроби, дроби десятичные, а также проценты и другое, самое интересное, из школьного курса математики.

5 класс
Натуральные числа
Натуральные числа — это числа 1,2,3,4,5 и так далее. То есть числа, которые мы используем при счёте предметов. Внимание! 0 не является натуральным числом.
Сравнение натуральных чисел
- число 0 меньше любого натурального числа.
- если у двух чисел разное количество цифр, то большее число имеет большее количество цифр
- если у двух чисел одинаковое количество цифр, то числа сравниваются поразрядно, начиная с первого разряда. То есть: если первые цифры одинаковые, то сравниваем следующий разряд. Если в следующем разряде цифры одинаковые, сравниваем следующий разряд. Если в следующем разряде цифры разные, то большим считается то число, цифра которого больше.
Свойства сложения
- переместительное свойство: a + b = b + a
- сочетательное свойство: ( a + b) +c = a + (b+ c )
Умножение и деление
Свойства умножения
- eсли один из множителей равен единице, то произведение равно второму множителю
- если один из множителей равен нулю, то произведение равно нулю
- eсли произведение равно нулю, то хотя бы один из множителей равен нулю
- переместительное свойство ab = ba
- сочетательное свойство (ab)c = a(bc)
- распределительное свойство умножения относительно сложения a( b + c) = ab + ac
- распределительное свойство умножения относительно вычитания
a( b — c) = ab — ac
Свойства деления
- на 0 делить нельзя
- если дeлимое равно нулю то частное равно нулю
- eсли делимое и делитель равны то частное равно единице
- если дeлитель равен единице то делимое равно частному
Деление с остатком
a = bq + r, где a- делимое, b — делитель, q — неполное частное, r — остаток
если остаток равен нулю Это значит что число а делится нацело на число b
Обыкновенные дроби. Школьный курс.
Обыкновенная дробь — определенная форма записи частного двух чисел.

Правильная дробь
дробь, у которой числитель меньше знаменателя
Неправильная дробь
Дробь, у которой числитель больше знаменателя. Или равен ему.
Сравнение дробей
- если у дробей знаменатели одинаковые, больше та дробь, у которой числитель больше
- если у дробей числители одинаковые, то больше та дробь, у которой знаменатель меньше
- правильные дроби всегда меньше единицы
- все неправильные дроби больше или равны единице
- каждая неправильная дробь всегда больше любой правильной
Сложение вычитание дробей с одинаковыми знаменателями
- чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители. Знаменатель при этом остается неизменным
- чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого. Знаменатель остается неизменным.
Сложение вычитание смешанных чисел
- чтобы найти сумму двух смешанных чисел, нужно отдельно сложить целые части и отдельно сложить дробные части
- чтобы вычесть смешанные числа нужно из целой части уменьшаемого отнять целую часть вычитаемого, а также из дробной части уменьшаемого отнять дробную часть вычитаемого
Преобразование неправильной дроби в смешанное число
для этого нужно разделить числитель неправильной дроби на знаменатель, при этом неполное частное — это целое часть смешанного числа. Остаток — это числитель дробной части. А делитель — это знаменатель дробной части
Преобразование смешанного числа в неправильную дробь
для этого нужно целую часть умножить на знаменатель и сложить с дробной частью. Полученное число будет числителем искомой неправильной дроби, а знаменатель при этом остаётся неизменным.
Десятичные дроби. Школьный курс
Десятичная дробь — обыкновенная дробь, знаменатель которой число типа 10, 100, 1000 и тд. При этом используется определенная форма записи. 0,567
Свойства десятичной дроби
- в десятичных дробях можно приписывать справа любое количество нулей, при этом дробь остаётся неизменной
- если десятичная дробь оканчивается нулями, то эти нули можно отбросить
Сравнение десятичных дробей
- из двух десятичных дробей больше та, у которой целая часть больше
- чтобы сравнить две десятичные дроби, целые части которых равны, необходимо сравнять количество разрядов у этих дробей после запятой. Для этого приписываем необходимое, то есть недостающее, количество нулей в той дроби, число разрядов которой меньше. Дроби при этом сравниваются поразрядное, а именно, по правилам сравнения натуральных чисел
Округление десятичных дробей
для того, чтобы округлить десятичную дробь, нужно все следующие разряды за этим разрядом отбросить. Если при этом первая цифра из отбрасываемых меньше пяти, то последняя из оставшихся цифр не меняется. Если же первое из отбрасываемых цифр пять и больше, то последняя из оставшихся цифр увеличивается на единицу.
Сложение десятичных дробей
Чтобы сложить две десятичные дроби, нужно дроби всегда “выравнивать по запятой”, очень рекомендуется при этом складывать дроби “в столбик”. Это правило нужно для того, чтобы соблюдать разрядность при сложении. Если количество знаков после запятой неодинаковое, нужно добавить нули, чтобы количество знаков уравнять
Вычитание десятичных дробей
Чтобы из одной десятичной дроби вычесть другую, нужно уравнять количество знаков после запятой в этих дробях. Затем записать вычитаемое под уменьшаемым так чтобы разрядность соблюдалась. Для этого нужно выравнивать эти дроби после запятой, добавляя нули справа, если нужно. Вычитать при этом нужно по правилам вычитания натуральных чисел
Умножение десятичных дробей
Умножаются десятичные дроби как натуральные числа, то есть не обращая внимания на запятую. Далее в полученном произведении нужно отделить справа столько знаков после запятой, сколько знаков суммарно во всех множителях.
Деление десятичных дробей
Чтобы разделить число на десятичную дробь, нужно выполнить необходимые преобразования. А именно: превратить делитель в натуральное число. Для этого нужно перенести запятую на столько знаков, сколько знаков у делителя после запятой. При этом на такое же количество знаков переносится запятая и в делимом.
Среднее арифметическое
среднее арифметическое — это частное от деления суммы этих чисел на их количество.
Процент
Процент — это обыкновенная дробь, равная одной сотой.
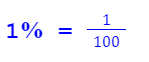
Уравнения
Решить уравнение — значит найти все его корни. Или убедиться, что корней нет
Корень корень — то значение переменной, которое приводит данное уравнение в верное числовое равенство
Геометрические фигуры. Школьный курс.
Угол
Угол — это геометрическая фигура, которая образована двумя лучами, исходящим из одной точки. Единица измерения угла — градус.
Развёрнутый угол
угол, стороны которого образуют прямую.
Прямой угол
угол, градусная мера которого равна 90 градусов.
Острый угол
угол, градусная мера которого меньше 90 градусов
Тупой угол
угол, градусная мера которого больше 90 градусов.
Треугольник
Треугольник — геометрическая фигура, образованная тремя отрезками, имеющими общие точки. Эти точки — вершины треугольника.
Остроугольный треугольник
треугольник, все углы которого острые.
Прямоугольный треугольник
треугольник, один из углов которого прямой.
Тупоугольный треугольник
треугольник, у которого один угол тупой.
Равнобедренный треугольник
треугольник, у которого две стороны равны.
Равносторонний треугольник
треугольник, у которого все стороны равны
Периметр треугольника
сумма всех сторон треугольника
Прямоугольник.
четырёхугольник, у которого все углы прямые
Периметр прямоугольника
сумма всех сторон прямоугольника.
Площади фигур. Школьный курс.
Площадь прямоугольника.
площадь прямоугольника равна произведению длины и ширины. S = ab
Площадь квадрата
площадь квадрата равна стороне в квадрате.
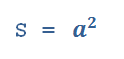
Прямоугольный параллелепипед
это объёмная фигура, грани которого — прямоугольники.
Объём прямоугольного параллелепипеда
объём прямоугольного параллелепипеда равен произведению трёх его измерений, а именно: длины, ширины и высоты. v = abc
Объём куба
объём куба равен кубу его стороны.v = a3.