Формулы сокращенного умножения

Формулы сокращенного умножения — формулы, применение которых сильно облегчает жизнь в алгебре и не только. Формулы очень полезные и очень понятные. Просто выводятся, легко запоминаются. Базовых, или основных, формул три.

Ранее мы уже разбирали различные преобразования и приемы в обращении с многочленами. Легко умножать многочлены, легко выносить за скобки общие множители. Так, опытным путем, много раз выполняя одни и те же (или похожие) действия, появились эти формулы. Они активно используются для преобразования многочлена в произведение. И наоборот, когда нужно быстро перемножить два двучлена, наприер. Итак.

Формулы сокращенного умножения. Квадрат суммы

При умножении многочлена на многочлен каждый член одного многочлена умножают на кадлый член другого многочлена. И, если умножаются два двучлена, можно просто воспользоваться формулой. Рассмотрим на примере. Если умножить (a+b) на (a+b), а точнее, возвести (a+b) в квадрат, то получим самую первую формулу сокращенного умножения, а именно, Квадрат суммы

Понять эту формулу и получить ее легко, необязательно запоминать, так как она легко «восстанавливается», но

Но важно уметь применять эту формулу, причем как прямо, так и обратно.

И словами, все для большего понимания

Рассмотрим на примере. Здесь «a» — это «8x», а «b» — «3».

Формулы сокращенного умножения. Квадрат разности

Теперь тоже самое, но для разности. Итак, возведем в квадрат разность двух членов.

эта формула получается аналогично квадрату суммы. Так как по сути это одна формула есть. Итак

И здесь также важно уметь использовать эту замечательную формулу в одном и другом направлении.

И словами.

И тоже рассотрим на примере. Здесь «a»- «10x», а «b»- «y». Итак

Формулы сокращенного умножения. Разность квадратов

Есть еще одна замечательная формула.

Попробуем эту формулу сотворить самостоятельно, то есть перемножить сумму и разность. Здесь (a +b) и (a -b). Итак

Итак. все просто. Необязательно запоминать. И также важно применять «наоборот». Также нужно натренировать свою «опытность» и «видеть» нужные алгебраические комбинации. Итак.

Словами.

На примере.

И наоборот.

Формулы сокращенного умножения. Сумма и разность кубов

Также, как и в предыдущем случае, формулы для кубов легко можно сотворить самостоятельно.

Рассмотрим на примере. Итак.

И рассмотрим на примере. Задание, например. Разложить на множители многочлен (двучлен)

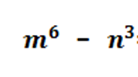
Чтобы справиться с этим заданием, надо увидеть здесь разность кубов. Для этого преобразуем выражение

Далее просто. Просто по формуле.

Формулы сокращенного умножения. Куб суммы и куб разности

Зная формулы квадрата суммы и квадрата разности, можно легко найти формулы кубов.