Рациональные выражения — выражения, которые состоят из выражений целых и выражений дробных. Целые выражения разбирались ранее. Дробные выражения разберем здесь.

Далее речь пойдет о дробных выражениях. При этом легко понять какие выражения (из представленных ниже) являются дробными.

Рациональные дроби. Рациональные выражения
Итак, дробными называются выражения, которые кроме сложения, вычитания, умножения, включают в себе деление. Причем деление на выражение с переменными. итак, такие выражения называются дробными. Если переменные заменить числовыми значениями, порлучим выраение числовое. При этом, целые выражения имеют смысл при всех значениях переменной, а дробное имеет смысл только в определенных условиях. Итак, целые выражения изучались ранее, а дробные выражения изучим подробнее. Имеет смысл дробное выражение только, если значения переменной не приводят к нулю значение знаменателя. Но очень важно, перед работой с дробным выражением необходимо проверить и найти значения переменных, которые приводят знаменатель к нулю, лишая тем самым дробноые выраение смысла. Итак, допустимые значения переменных.

Итак, выражение вида
называют дробью. При этом знаменатель дроби (b) не долен равняться нулю.
Таким образом,

И, важно, допустимые значения переменной — все значения, кроме тех, которые допускают B=0.
Итак, при работе с рациональной дробью (с рациональными выражениями) всегда сначала проверяется (находится) область допустимых значений. То есть необходимо найти недопустимые значения переменных, приравняв знаменатель дроби к нулю.
Основное свойство рациональной дроби. Сокращение дробей
Важно.Вспомним основное свойство дроби из курса математики.
Основное свойство дроби
Если числитель и знаменатель дроби умноить на одно и то же натуральное число, то значение дроби не изменится
То есть при любых натуральных значениях a,b и c верно равенство
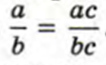
Это свойство работает и для рациональных дробей, на определнных условиях, конечно же. b и c — ненулевые многочлены. Итак, основное свойство рациональной дроби.

Например

но важно, x не должен равняться нулю и x не должен быть равынм -y. И важно еще другое. Это равенство равно при всех допустимых значениях переменных. Такие равенства называются тождествами, а преобразования — тождественно равными.

Ранее тождествами называли равенства, равные при всех значениях переменных. Здесь необходимо внести поправки. Только при допустимых значениях переменных. Основное свойство рациональной дроби позволяет приводить дроби к другому знаменателю, а также сокращать.
Итак, сокращение дробей.
Если
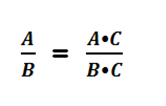
то верно и обратное

При этом происходит сокращение дробей. Разберем на примере.
Пример. Постройте график функции
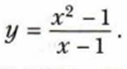
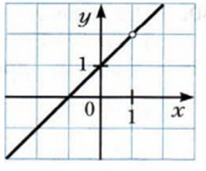
Область определения функции — все значения переменной, кроме x равной одному, при x =1, знаменатель становится равным нулю и рациональная дробь не имеет смысла. Сократим рациоанльную дробь:

Итак, искомым графиком функции являются все точки прямой y= x+1, но за исключением одной точки, абсцисса которой равна 1.
Сложение и вычитание рациональных дробей. Рациональные выражения
- Сложение рациональных дробей с одинаковыми знаменателями
Как и в предыдущей главе, сначала вспомним, правила сложения обыкновенных дробей.
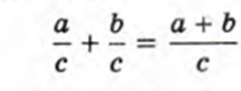
и также, как в главе предыдщей, подытлоим, что дроби рациональные складываются тоже также. То есть, если знаменатели одинаковые, числители складываем, знаменатели оставляем.

Например, сложим рациональные дроби
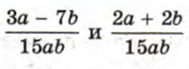
Итак,

Все просто. Очевидно, что вычитаются рациональные дроби аналогично.
Например, вычтем из дроби дробь
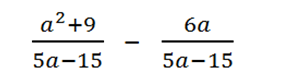
итак

- Сложение рациональных дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями сводится к поиску и приведению к одному знаменателю. И в итоге складываются дроби со знаменателями одинаковыми. По правилам сложения обыкновенных дробей. При этом поиск общего знаменателя — бесконечно увлекательный и очень творческий процесс.
Рассмотрим на примере. Сложить дроби

И еще пример. Вычитание.

Здесь общий знаментель находится чуть дольше, для этого сначала выполним необходимые преобразования

Итак, теперь общий знаменатель, очевидно, -произведение трех множителей: a, b и (a+b), то есть вспомогательный множитель первой дроби — b, второй -a. Итак

Умножение и деление рациональных дробей
Умножение и деление рациональных дробей выполняется по правилам умноения и деления дробей обыкновенных. Итак, умножение дробей
- Умножение рациональных дробей
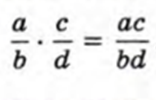
Очевидно, дроби рациональные умножаются по тем же правилам. то есть

Но правило умножения рациональных дробей работает не только для двух дробей. Итак, если A, B,C,D,P и Q- многочлены,

Все просто, намного проще, чем сложение дробей с разными знаментелями. Рассмотрим на примере

Еще пример, посложнее. Умножим дробь на многочлен. Итак

- Деление дробей
Деление рациональных дробей, также, как и умножение, как и сложение выполняется по правилам обыкновенных дробей. Итак, чтобы поделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
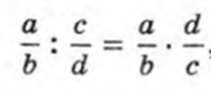
Итак, если A, B, C, D — ненулевые многочлены, то правило деления рациональных дробей

Или правило

Например,

Или

И «посложнее», деление дроби на многочлен. Представим многочлен в виде рациональной дроби. Итак









