Уравнения. Это всегда. Это навсегда. Любимое.

Линейные уравнения
Этот вид уравнений мы уже изучали в разделе «математика«. Остается только добавить, что они имеют вид:

Или же ax + b = 0, где k и b — ненулевые числовыекоэффициенты. Решаются просто.

На примере:

Все ур. первой степени сводятся к уравнению вида ax + b = 0 и решаются легко. А именно,
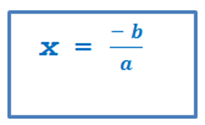
Все.
Системы линейных уравнений
Системы линейных уравнений решаются тремя способами, а именно: метод подстановки, метод сложения и графический способ. Итак, рассмотрим все три.
- Способ подстановки
Решим систему уравнений методом подстановки

Метод подстановки заключается именно в использовании подстановки в ходе решения. Итак.

Итак, одна переменная известна, теперь подставляем ее значение в уравнение и находим другую переменную, при этом подставлять можно в любое уравнение. Но, очевидно, в первое уравнение лучше. Так как проще.

Итак, система решена. Так как прием и основная техника — подстановка, (выражаем переменную одну через другую и подставляем во второе уравнение вместо переменной полученное выражение), данный способ носит название «способ подстановки».
Итак, алгоритм решения систем уравнений методом подстановки

- Способ сложения
Решим систему уравнений методом сложения.

В этой системе коэффициенты при y — противоположные числа, поэтому система уже готова к сложению. То есть при сложении двух уравнений переменная y «уйдет». Итак. Складывем два уравнения и получаем:
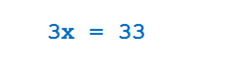
Решаем полученное уравнение, находим переменную x=11 и подставляем ее в уравнение

Система решена. Итак, x = 11; y = -9.
Но это была легкая, очень удобная система. Здесь изначально были «поданы» коэффициенты, которые являются противоположными числами. Рассмотрим случай посложнее, когда нужно с системой «поработать».
Итак. Новая система.

если в такой системе сложить уравнения, это не приведет к успеху, так как переменная «не уйдет». Чтобы избаиться от переменной, нужно с этой системой поработать. Сначала нужно определить какую переменную «будем убирать». Здесь нужно руководствоваться здравым смыслом и идти по самому легкому пути. Очевидно, в этой системе проще убрать x, для этого нужно первое уравнение умножить на «минус два». Итак.
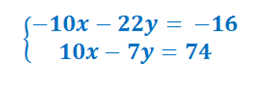
Теперь складываем уравнения. Получаем
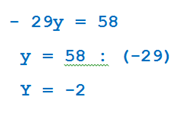
Далее подставляем значние переменной в одно из уравнений и находим вторую переменную x. Очевидно, x = 6
Система решена, но и это не самый сложный случай. Рассмотрим систему, где преобразования нужны для двух уравнений. Итак.

На самом деле, случаи и системы бывают разные и всегда любую систему можно решить любым способом. Кому ближе метод сложения, выбирают сложение, подстановку твыбирают любители подстановки. Итак. Алгоритм решения системы методом сложения.

Графический способ решения систем уравнений
Чтобы решать системы линейных уравнений у нас уже есть два прекрасных способа. Но есть еще один, он заслуживает отдельной главы, так как он необычен и принципиально отличается от двух других. Итак. Повторим


Очевидно, что иногда уравнения и системы уравнений не имеют решений. Здесь — то и особенно хорош этот способ, так как наглядно показывет, если решений нет. Или же решений бесконечно много.
Линейное уравнение с двумя переменными можно посторить. Это линия, для построения которой нужно преобразовать уравнение и привести к виду y= kx + b, далее обыновенные построения по двум точкам.
Вся соль метода заключается в том, что строятся две линейные функции и находится точка их пересечения. Это и есть решение системы, то есть координаты точки — корни уравнений x и y.
Так как графиками уравнений, входящих в систему, являются прямые, то возможны три сценария:

Заметим, что первое, что отмечается, а иногда и единственное, — это именно количество решений системы.
Рассмотрим на примере. Решим графически ситему.
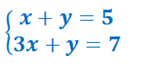
Для построения необходимо преобразовать оба уравнения:
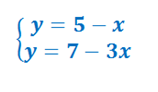
Теперь построим график функций y= 5 — x и y = 7 — 3x. Построению графиков мы научились ранее, поэтому сразу перейдем к графическому решению.
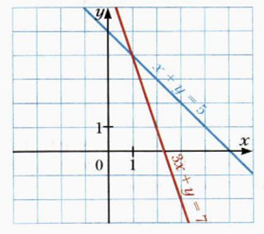
Точка пересечения графиков есть и ее кординаты — (1; 4), проверим, подставив в уравнения:
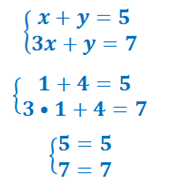
Итак. Алгоритм решения системы графическим способом.

Алгебраическое решение задач (с помощью уравнений)
Невозможно описать точно способ решения задач алгоритмически, здесь важен опыт и энтузиазм, так как именно с помощью уравнений чаще всего и проще всего решаются большинство задач. И именно этот способ самый любимый. Нет универсального способа, но есть алгоритм, вот он:

Это все, что нужно знать и уметь, чтобы решать задачи. Попробуем разобрать на некоторых примерах. В задачах приводится только составленное уравнение.
Например, задача:

Для решения задачи составим математическую модель, чтобы затем решить задачу двумя способами.

Итак, теперь второй способ. Если два неизвестных — две переменные, составлять их проще.

Но решить такое уравнение невозможно (если только подбором), поэтому здесь нужна система уравнений.
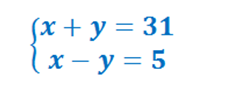
Решение систем линейных уравнений разобрано подробно выше.








