Координаты точки. Координатная прямая. Координатная плоскость. Декартова система координат или прямоугольная система координат. Названа по имени Декарта. Общепринятая система для обозначения местоположения точек в пространстве. Здесь остановимся на двумерной системе. Начнем сначала, а именно, с луча. Координатного луча.

Координаты.Координатный луч
В повседневной жизни часто пользуемся различными измерительными приборами, где для измерений или снятия показаний существуют шкалы. Шкалы с ценой деления. Так каждый штрих подразумевает под собой какое — то минимальное измерение, единичный отрезок. В начальной школе изучаются (с успехом) простейшие геометрические фигуры. Так к пятому классу, к первому классу старшей школы дети уже легко оперируют такими понятиями как прямая, луч, отрезок и хорошо отличают одно от другого. Поэтому легко вводится такое понятие как луч координатный. Итак

Координатный луч. Похож на линейку, только нет единиц измерения.

Все такое же. Нуль. 1, 2, 3, и далее. Но есть простор для фантазии, так, если мы сами задаем координатный луч, то сами задаем и единичный отрезок. Так получаем свои, отличные от других «картинки». Итак, основные понятия. Точка О. Начало отсчета. Далее. Единичный отрезок.

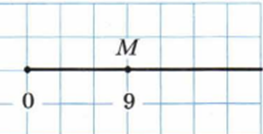
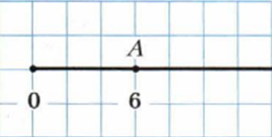
Координаты точек записываются строго в определнном порядке. А именно; F(7), например. Или как на рисунке: M(9)— точка М с координатой 9. А(6) — точка А с координатой 6.Но иногда упрощают и говорят число. «Отметим число»
Координаты.Координатная прямая
Координатная прямая, важно, что координатная прямая — прямая, на которой обозначили начало отсчета, направление и единичный отрезок.

Также, как и луч, несет свои геометрические свойства, то есть бесконечна в любом направлении. Также. как и координатный луч, имеет начало отсчета. обязательный единичный отрезок и направление. Есть принципиальное отличие, и теперь все уже по-взрослому, появляется область отрицательных чисел. Итак.

в обозначении координат ничего принципиально не меняется, кроме того, что добавляются точки с отрицательными координатами. Так, например: А(-2); P(-6); K(-7); M(-9). Точка А с координатой «минус 2» и далее.

Здесь же вводим понятие противоположных чисел. Точки А и В — точки с противоположными координатами. То есть числа 2 и -2- противоположные.
Числа, одинаковые по значению, но разные по знаку называются ПРОТИВОПОЛОЖНЫМИ.

Здесь же полезно вспомнить модуль, так как модуль — расстояние от точки до начало координат.
Координатная плоскость
И, наконец, координатная плоскость. Две перпендикулярные прямые. Тоже начало отсчета и тоже единичный отрезок. Оси x и y.

Что принципиально важно, что отличает плоскость от координатной прямой — две прямые. Две координатные прямые и теперь координату точки определяют две коордианты. По оси x и по оси y.
Итак, теперь координаты точки обозначаем: A(3; 3), где первое число — координата на оси x, второе число — координата на оси y.

Итак, координата точки A(3;3). Точка А с координатами «три,три». На рисунке А (А1; А2).
И важно, координатная плоскость прямыми разделена на четыре угла. или на четыре четверти. Обозначаются они римскими цифрами I, II, III, IV и считаются с правого верхнего угла.

Диаграммы
Теперь можно строить графики, диаграммы и наглядно изображать любые статистические данные. Так, например, график температур на графике гораздо симпатичнее, чем в обычной таблице.

Информация читается проще, быстрее и увлекательнее, очевидно. Или скучная задача про крыши, например, тоже становится зрелищной и понятной. Графики читаются легче, информация получается нагляднее.

В поселке было 90 домов. Из них под черепичной крышей — 45 домов, крыша шиферная у 30 домов, а железная у 15. Теперь про крыши мы знаем все.







