Простейшие экономические задачи часто встречаются на экзамене. Эти задачи необходимо разобрать и научиться легко решать их. Для повышения мотивации можно вспомнить, что задачи такого типа часто встречаются в жизни. Так мы часто выбираем где лучше скидка, а также много фантазируем на тему приумножения капитала, поэтому, чтобы преуспеть в этом вопросе, весь свой досуг рекомендую заполнить решением экономических задач. Итак, начнем
Эконoмические задачи. Немного теории
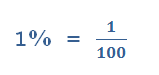
Чтобы найти % от числа, надо процент, представленный десятичной дробью, умножить на число. А именно:
«Чтобы найти дробь от числа, надо число умножить на эту дробь»
«Чтобы найти дробь от числа, надо число умножить на эту дробь»
- НЕМНОГО ПРО ВКЛАДЫ
Если число увеличилось на х процентов, то это число и увеличилось в какое-то количество раз.
Итак. Пусть число y увеличивается на x%
Получаем: х + 0,01yх = (1 + 0,01y)x
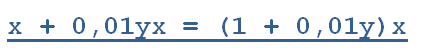
Если это экономическая задача и действие разворачивается в банке, некая сумма y кладется в банк под х%, то после первого года будет (1 + 0,01y)x
Через еще один год (1 + 0,01y)•(1 + 0,01y)x
(1 + 0,01y)•(1 + 0,01y)•(1 + 0,01y)x
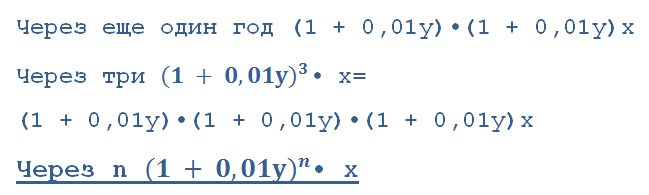
Экономические задачи. Немного практики
Так можно просто решить любую (простую) экономическую задачу. Например,
если знать эту прекрасную формулу. Итак
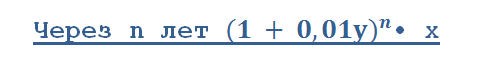
- ЗАДАЧА

Зная формулу, можно просто подставить все известные величины и найти неизвестные.
Здесь n=5, x = 20, y = 50000, итак:
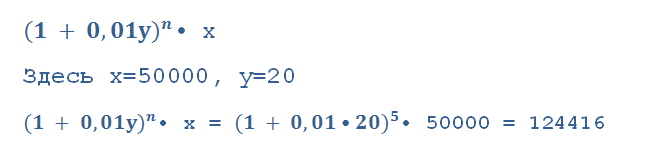
- ПОПУЛЯРНАЯ ЗАДАЧА
Например, про пальто. Но герой может быть любой. Главное, чтобы этот герой, а точнее его стоимость была немного волатильной. Ох, популярный нынче термин. Итак, пальто

Первое, что приходит на ум — цена вернется. Но в этом и «подвох»…Рассмотрим решение:
Например, пальто первоначально стоило 100 рублей, всегда можно применять такой способ решения «например, цена была такой-то..». Итак. После увеличения на 20% пальто будет стоить 120 рублей. Теперь стоимость пальто уменьшается на 20 % и цена становится:
120 – 0,2•120 = 96. Резюмируем:
При увеличении стоимости 20% и последующим снижением стоимости на тот же процент, стоимость уменьшится на 4%.
Попробуем решить задачу без конкретных цифр.
Пусть некий товар стоил y рублей. Затем его стоимость увеличилась на х%, а потом снизилась на тот же х%. Получаем:
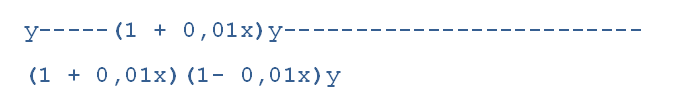
Нетрудно доказать

При этом процент может быть неодинаковым при увеличении и снижении. Например.
Пусть цена товара будет y

Что и требовалось доказать. Все просто. Просто и полезно.








Right here is the perfect webpage for everyone who would like to understand this topic. You understand a whole lot its almost tough to argue with you (not that I really will need toÖHaHa). You certainly put a fresh spin on a subject that has been discussed for a long time. Wonderful stuff, just excellent!
Can I simply say what a comfort to find someone that actually understands what theyre discussing on the net. You actually realize how to bring a problem to light and make it important. More and more people really need to read this and understand this side of your story. I was surprised that youre not more popular since you definitely possess the gift.
Thanks