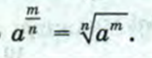Степени. Свойства степеней. Как часто мы используем их. Как часто мы используем их в алгебре. В повседневной жизни мы часто повторяем одни и те же действия по много, много раз. Часто именно в повторении сила и красота. Всегда мощь и результат. В математике для часто повторяющихся операций вводится дополнительные символы. Степени — один их них. И, если мы любим перемножать один множитель на себя. Же, без степени не обойтись. Итак.

Что такое степени
Произведение нескольких одинаковых множителей. Например

Итак. Определение.

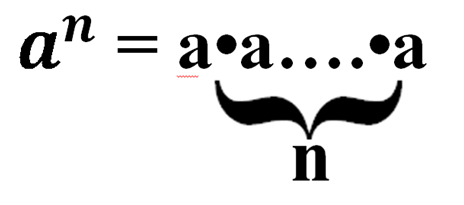
Нахождение значения — возведение в степень. При этом a — основание степени, n- показатель степени.

Важно. При возведении в степень отрицательного числа результат может быть отрицательным или положительным. Например.
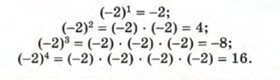
Степень отрицательного числа с четным показателем — число положительное.
Степень отрицательного числа с нечетным показателем — число отрицательное. То есть

Умножение и деление степеней.
При умножении степеней с одинаковыми основаниями(!!!!!) основание остается прежним, а показатели складываются. При делении степеней основание остается прежним, а показатели вычитаются. Итак

Итак, формула.

При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются. То есть

Если это правило применить для одинаковых степеней, то можно вывести новую формулу. Итак.

Так как
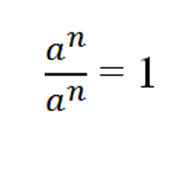
Важно!! Это нужно запомнить. Хотя, конечно, это очевидно тоже

Возведение произведения в степень
Для любых a и b и натурального числа n справедлива следующая формула

Эта формула тоже легко выводится. Итак.

Или рассмотрим общий случай. По определению

Доказанное свойство степени произведения распространяется на степень трех и более множителей.
Возведение степени в степень
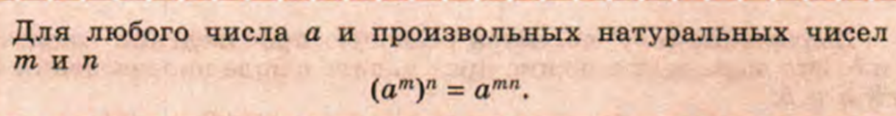
Попробуем эту формулу вывести.

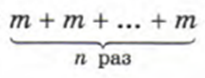
Теперь заменим сумму произведением mn


Итак. При возведении степени в степень, основание остается прежним показатели перемножаются.
Степень с целым отрицательным показателем
Для любого числа a, не равного нулю, и натурального числа n, верно равенство
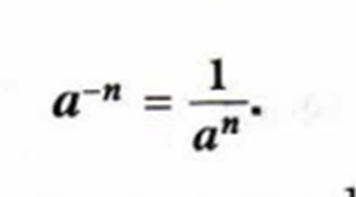
Выражение не имеет смысла при n=0

Стандартный вид числа

Стандартный вид числа — запись числа в виде произведения

где n — целое число и соблюдается следующее условие

Число n называют порядком числа, записанного в стандартном виде. Стандартный вид числа используется для компактной записи больших или очень малых чисел (масса солнца и масса атома водорода, в килограммах, например)
Степень с целым показателем
Коротко и ясно
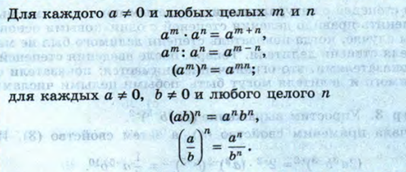
Степень с рациональным показателем
Если a- положительное число, m- целое, n- натуральное число, то степенью с рациональным показателем будем называть