Дробь обыкновенная. Сложение дробей. Вычитание дробей.

Дробь обыкновенная. Это ЧИСЛО. ДОЛЯ. Обозначает часть чего-либо. Еще бывают дроби десятичные. Имеют другой вид, разное применение и отличия в использовании. Обыкновенная дробь впервые появляется в пятом классе, на уроках математики.

Дроби или дробные числа записывают с помощью двух натуральных чисел и дробной черты, используют дроби, чтобы обозначить что-то дробное.

Дробь это

Число. записанное с помощью двух натуральных чисел и черты. число, записанное над чертой, — числитель дроби. Обозначает сколько взяли. Число, записанное под чертой — знаменатель — на сколько разделили.

На примере. Три четвертых. Что-то поделили на четыре части. Взяли только три.

  

Дроби правильные и неправильные

Дробь правильная и неправильная. Если числитель меньше знаменателя (взяли меньше, чем всего частей). дробь правильная. Если взяли больше, чем всего частей, то неправильная. Как это возможно?

Смешанные числа

Если дробь неправильная, то это можно исправить. Всегда дробь можно привести в правильный вид. Для этого нужно выделить целую часть и отделить ее от дробной. Для неправильных дробей придумали отдельную форму записи и отдельное название. Итак. смешанные числа.

Нетрудно догадаться и выделить целую часть из дроби. Потому что по знаменателю понятно на сколько частей поделили нечто. Именно столько частей в каждой целой части. Ведь целая часть или ОДИН — это отдельный вид неправильной дроби, когда числитель равен знаменателю. То есть

где m — натуральное число. При этом m- любое натуральное число. Так мы можем поделить наше нечто на ЛЮБОЕ количество кусочков. Чтобы легко превратить неправильное число в смешанное, нужно вспомнить деление чисел «в столбик». И вообще, дробь и есть деление. Итак. делим числитель на знаменатель, получаем неполное частное и остаток. Частное- наша целая часть, остаток- числитель дробной. Пример. Всего на рисунке три пиццы. Три пиццы или 24 кусочка, каждую пиццу порезали на 8 кусков. 24/8 Или

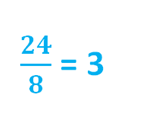
Или десять восьмых. Десять кусочков (выделены на рисуне) из 8 возможных (всего кусочков из одной пиццы)

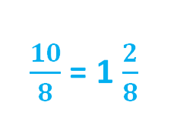
Еще пример и еще один способ получить правильную дробь (смешанное число) из неправильной.

Дробь обыкновенная. Сложение и вычитание дробей

Итак. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить числители. Знаменатели при этом остаются без изменений. Сложение и вычитание дробей с одинаковыми знаменателями. все очень просто. числители складываются, знаменатели оставляем без изменений. На примере.

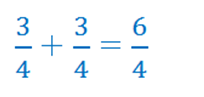
При этом. если в ответе получилась неправильная дробь, можно преобразовать ее в смешанное число. вычитание происходит аналогично. А теперь перейдем к дробям с разными знаменателями. Для этого начала вспомним про основное свойство дроби. Это базовое правило( закон) при использовании дробей. Итак, основное свойство дроби.

Дробь обыкновенная. Основное свойство дроби

основное свойство дроби

Если числитель и знаменатель умножить на одно и то же натуральное число, то получится равная ей дробь

Итак, это основополагающие правила «работы» с дробями. Если встречаются дроби с разными знаменателями, без основного свойства дроби не обойтись.

Важно.

Сложение дробей с разными знаменателями.

Ключевая фраза. Складывать дроби можно только с одинаковыми знаменателями, при этом складываются только числители.

Если знаменатели разные, нужно дроби привести к одному знаменателю. Для этого знаменатели подбираются «без подручных средств» или же с использованием НОК и НОЗ. НОК – наибольшее общее кратное. 

На примере. Найдем общее кратное чисел 24 и 36.

24: 24; 48; 72; 96; 120; 144 и т,д

36: 36; 72; 108; 144; 180 и т.д.

Видно, что у чисел  24 и 36 есть общие кратные – 72 и 144, наименьшее из которых – 72. Значит у дробей со знаменателями 24 и 36 можно «подобрать» общий и привести к нему обе дроби.         Итак, НОК/НОЗ(24;36) = 74

Сложение и вычитание дробей . Алгоритм нахождения НОК для двух чисел.

Для начала нужно вспомнить разложение на простые множители. На примере числа 210

Или числа 756

Чтобы найти НОК числе 210 и 756, нужно выписать все множители числа 210 и добавить к ним недостающие множители числа 756

Итак НОК(210;756)= 3•7•2•5 •3•3•2 = 3780

НОЗ (210;756) = НОК (210;756) = 3780

То есть, применяя для дробей с такими знаменателями получим следующее:

Здесь для дробей со знаменателями 84 и 90 нетрудно провести необходимые преобразования.

На примере

 и далее дроби, теперь с одинаковыми знаменателями складываем по уже понятному алгоритму.

Дробь обыкновенная. Сокращение дробей

Деление числителя и знаменателя на общий делитель. Это есть сокращение дробей.

Дробь обыкновенная. Умножение дробей

умножение дробей

Чтобы умножить дробь на дробь, нужно числитель умножить на числитель. а знаменатель умножить на знаменатель

Чтобы умножать смешанные числа, нужно сначала перевести эти числа в дроби. Итак, неправильные дроби, конечно же. Сокращение дробей здесь — обязательно!! На примере

Теория закончилась. Поэтому теперь остальное — прекрасная и удивительная практика.

Дробь обыкновенная. Деление дробей

Деление дробей

Чтобы поделить одну дробь на другую. надо первую дробь умножить на дробь. обратную второй.

Важно. Чтобы поделить смешанные числа. нужно сначала преобразовать смешанные числа в неправильную дробь. Смешанные числа. При делении, также, как и при умножении, требуется преобразование в неправильную дробь

На этом все. Теперь только практика. столько практики и тренировок, сколько нужно. Все индивидульно.