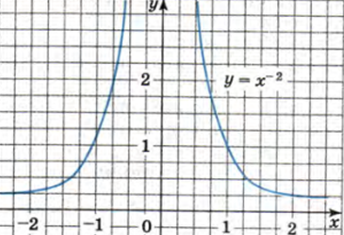
Функции. Функциональная зависимость. Все процессы в мире, а также любые взаимодействия влекут за собой изменение всех участников процессов. При этом один участник всегда ведущий. Тогда другой всегда зависим. То есть зависит от изменений первого. Практически все в мире, или почти все, можно описать математически. Так или иначе математитеские модели подводятся под многие процессы в природе и других областях

Функция. Что это такое.
В алгебре под фукцией понимается отношение между величинами. Или другими словами зависимость. То есть так как в математике связь между площадью и длиной стороны, скоростью и временем, стоимостью и ценой покупки и др. И тогда в этом случае зависимость можно описать или задать. Поэтому в дальнейшем мы будем называть и определять эти зависимости. Функция или функциональная зависимость между величинами.
- Способы задания функции
Функция задается разными способами. Это описание, таблица, график и формула. Однако самым распространненым считается способ задания с помощью формулы. Формула позвляет для любого заданного значения независимой переменной найти значение переменной зависимой. При этом независимая переменная называется аргументом, а зависимая — функцией. Важно. Все возможные значения аргумента образуют область определения, все возможные значения функций — область значений.
- Способы задания функции. С помощью формулы
Итак. Самым распространенным считается способ задания функций спомощью формулы. Но сильно реже функции задаются с помощью описания. Описывают функции словами, текстом в том случе, когда другой способ затруднителен или невозможен. это самый непрактичный способ, но самый простой и понятный.
Описываются функции также с помощью таблицы. например

- Способы задания функции. С помощью графика
Итак.Также функции задаются графиком. Например
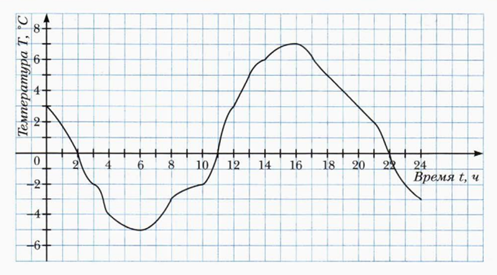
Но, как уже отмечалось выше, чаще всего и привычнее всего функции задаются формулами. Например, знакомые нам с начальной школы S=vt, P= 2(a+b), S= ab и другие.Часто встречаются, поэтому с функциями, заданными аналитически, с помощью формулы остановимся позже и подробнее.
Графики функций
Графики функций
График фукции — множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

- Построение графика
Чтобы построить график, нужно задать ( просто придумать) значения аргумента( независимую переменную),обозначаемую x. Затем подсчитать значение функции по формуле. Для этого каждый раз подставляем значения x в формулу, чтобы вычислить y. Итак получается необходимое множество точек. Но важно помнить, что эти значения x и y есть координаты точек. Итак всегда для построения графика сначала создаем таблицу значений. Например.

Найденные координаты точек указываем на координатной плоскости. Так получаем то самое множество точек, которое и есть график фукции.
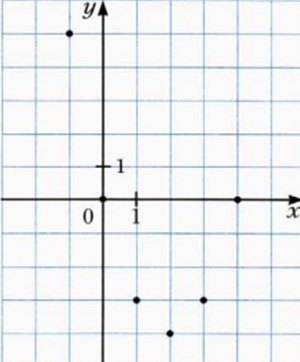
Здесь обозначено минимальное количество точек. Количество может быть любым, так как точек много не бывает. Чем больше точек, тем точнее график. Все зависит от поставленной цели. все зависит от желания. Все зависит от тебя.
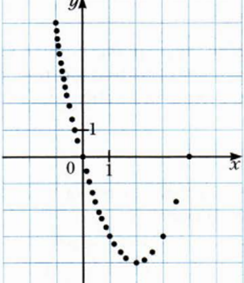
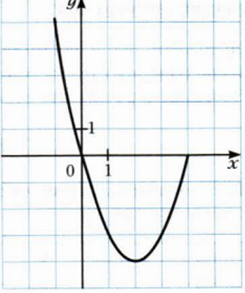
Дальше рассмотрим самые популярные и самые востребованные функции. А именно. Линейная функция. Чаще других используется. Раньше других изучается. Легче всего для понимания. Требует для построения всего две точки. Всегда прямолинейна. Квадратичная функция. Тоже очень популярная. Тоже неприхотлива в использовании. Довольна мила на вид и очень практико-значима. Обратная пропорциональность и функция степенная реже встречаются. Очень капризны и сложны в построении, есть нюансы при применении. Поэтому обо всем по порядку.
Линейная функция
Это самая популярная. Самая простая в использовании функция.
Линейная функция
функция, которая задается формулой y=kx + b, здесь x- независимая переменная, k и b — коэффициенты
- График функции
Важно. Область определения — все числа. Область значений — все числа. График- всегда линия. Конечно же!! Функция линейная. же. Итак. Построим на примере. Например,линейная функция y= — 2x + 1. Сначала таблица значений.

Важно. Для построения прямой нам нужно всего две точки. Поэтому для построения такое количество точек необязательно. Итак.
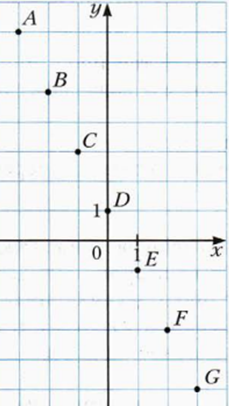
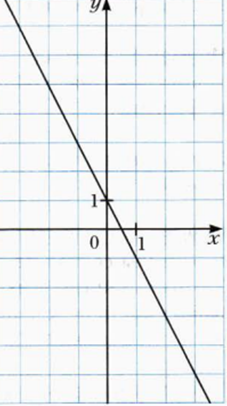
- Коэффициенты линейной функции
Заметим. Расположение прямой на плоскости зависит от значений коэффициентов k и b. Рассмотрим все случаи. Важно. за угол наклона «отвечает» угловой коэффициент k. Но и коэффициент b тоже активно участвет в построениях. Поэтому на графике всегда легко увидеть его значение. Так как пересечение графика линейной функции с осью Oy всегда в точке (0,b). Итак значение b всегда можно «взять» из графика. И нетрудно догадаться почему. Так как функция y= kx +b при х = 0 равна b. То есть при x=0 y=b. Итак точка (0;b). И эта же точка есть точка пересечения графика с осью y. Кстати, при построении графика линейной функции всегда рекомендуется «выбирать» точки пересечения с осями. Но вернемся к анализу коэффициентов.
Итак. Знак и значение углового коэффициента хорошо видно на рисунке.
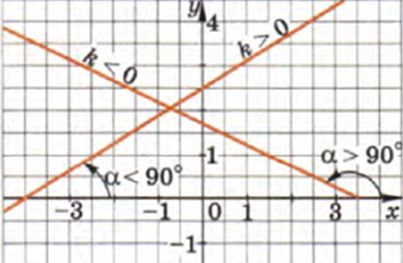
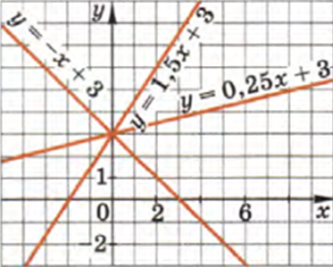
- Угловые коэффициенты.
Угловые коэффициенты
если угловые коэффициенты у линейных функций равны, то прямые параллельны. А если различны, то прямые пересекаются

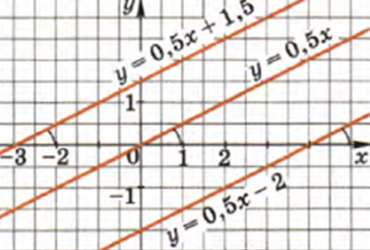
Если угловой коэффициент k=0, то функция параллельна оси x. Все верно. Если k=0, y= kx + b = b. На примере
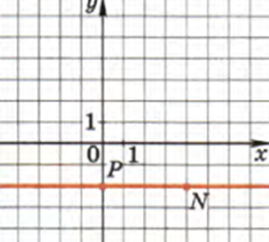
Линейная фукция.Прямая пропорциональность
Если коэффициент b=0, то линейная функция y=kx называется прямой пропорциональностью и несколько отличается в построении графика. Так как график прямой пропорциональности проходит через точку (0;0),то это и есть принципиальное отличие его от функции линейной. Которая не проходит через начало координат. Рассмотрим на графике.
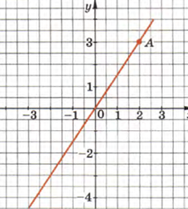
Заметим. Функция y= kx всегда пересекает начало координат (точку (0;0)), поэтому для построения графика достаточно задать только одну точку. Так на рисунке для построения графика y= 1,5x возьмем x= 2. Тогда y= 1,5x= 3. Так получаем точку А(2;3). Все остальные свойства прямой пропорциональности, такие же, как и у линейной. А именно влияние знака и значения углового коэффициента на расположение и вид графика такие же,
Квадратичные функции
Функции — тема очень интересная и требует особого внимания. То есть требует внимания и более детального изучения, анализу графиков и изучению свойств функций посвятим отдельную главу и много внимания. Итак, квадратичная фунция. Знакомство.

График квадратичной функции -парабола. Построить график функции можно тремя способами.
- Первый способ построения графика. Табличный.
Первый, обычный, то есть привычный.Табличный. То есть здесь нужно просто задать значения
x. Или аргумента. Затем вычислить значения y. Для примера возьмем самую распространенную функцию. область определения — все числа. Область значений — только положительные значения y.

Итак. график функции

- второй способ построения графика
Для второго способа рассмотрим сначала следующую функцию
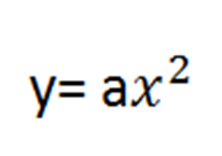
Коэффициент a играет важную роль. Также как и у линейной функции, знак коэффициента «отвечает» за расположение графика, а точнее, направление ветвей параболы. То есть направление ветвей вверх или вниз. Итак. Значение коэффициента «отвечает» за полноту. Чем больше значение коэффициента, тем ближе график к оси y.
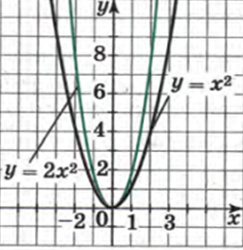
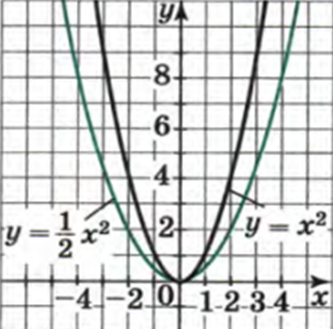
И еще. Знак коэффициента. Рассмотрим. a= 1/2 и a=-1/2. Хорошо видно. Если коэффициент отрицательный, ветви параболы направлены вниз. и наоборот. Если коэффициент положительный, ветви расположены вверх.
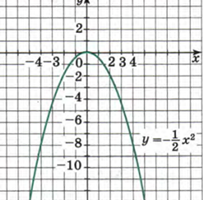
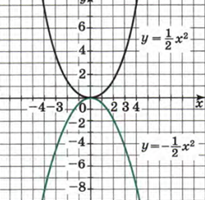
Но более сложные случаи рассмотрим подробно в следующей статье.
- третий способ построения графика
Разберем третий способ. По формуле вершины. Итак, формула для нахождения координат вершины параболы. Для функции
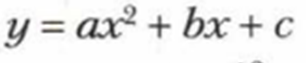
Итак. Координаты вершины
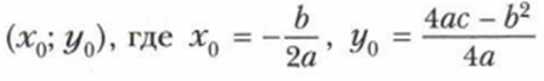
Вообще, график квадратичной функции будет по форме похож на график функции
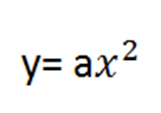
Но расположен на «своем» месте. Итак, алгоритм построения квадратичной функции через поиск координат вершины параболы.

Изучение графиков квадратичной функции увлекательно и очень полезно. Потому что помогает при решении квадратных уравнений. Не только поэтому очень рекомендую свою статью. Она целиком о графиках квадратичной функции.
Функции. Обратная пропорциональность
Обратная пропорциональность — понятие, с которым мы все сталкиваемся в школьном курсе математики. и в жизни, конечно! Потому что не все в жизни прямо пропорционально.Например, изучая математическую модель движения транспортного средства, имеем прямую пропорциональность в зависимости расстояния от времени( при постоянной скорости). И еще обратную пропорциональность в зависимости скорости от времени( при постоянном расстояни и). Все просто. Чем больше время,тем больше расстояние. Очевидно. Здесь это Прямая пропорциональнсть. Чем больше скорость, тем меньше время. Обратная пропорциональность. Итак.
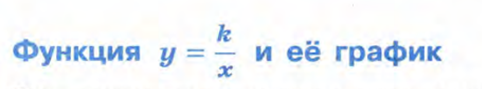
Обратной пропорциональностью можно назвать функцию вида y= k/x. Здесь x- независимая переменная. k- коэффициент пропорциональности. k не равен нулю. Область определения — все числа, кроме нуля. Рассмотрим график функции на примере. y= 12/x. Итак. таблица значений.

Теперь отметим все координаты точек (1;12), (1,5;8), (2;6). И далее на координатной плоскости. Для наглядности сразу же проанализируем свойства функции. А также отличия графиков у функции y= -12/x
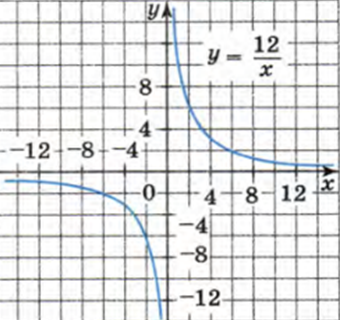
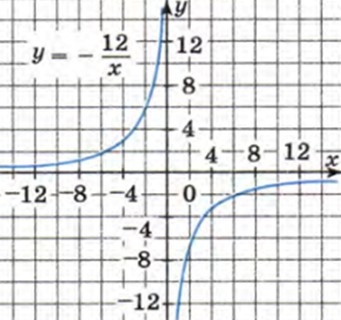
Графики представляют собой кривые. Это кривые, которые состоят из двух ветвей, симметричных относительно начала координат. НЕтрудно догадаться, что знак коэффициента влияет на расположении кривых. Так, при k больше нуля, гипербола (так называется график обратной пропорциорнальности) лежит в I и III четверти. При k меньше нуля, гипербола лежит во II и IV четвертях. Итак.
Гипербола
Кривая. являющаяся графиком обратной пропорциональности, называется гиперболой. Гипербола состоит из двух ветвей.
Степенная функция
Итак. Функции, которые можно задать с помощью степени, называют степенными.
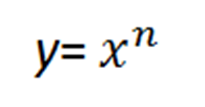
. Рассмотрим самую известную и часто применяемую функцию. А именно, — функцию квадратичную. Она заслуживает отдельной статьи. А также функция третьей степени, также часто применяется.
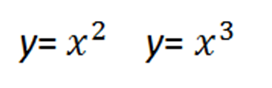
Есть еще функции. которые мы уже изучили в этой статье, но они также могут быть представлены в этом разделе. Это функции вида
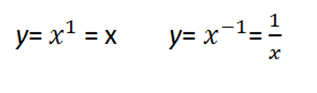
Далее для кругозора и повышения мотивации рассмотрим функцию
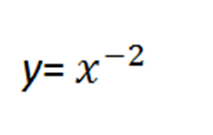
Эта функция также расположена выше оси x. И также симметрична. так как аргументам с разным знаком соответствует одинаковые значения фукции. Но немного «оригинальна»