
Треугольник — геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и отрезков, соединяющих эти точки.
Треугольники. Виды треугольников
Треугольник — базовая фигура в геометрии. Треугольники отличаются по типу углов и сторон. Итак. По типу углов.Треугольники бывают остроугольные, прямоугольные и тупоугольные.
По размерам сторон. Треугольники бывают разносторонние, равносторонние и равнобедренные.
Остроугольный треугольник Прямоугольный треугольник Тупоугольный треугольник

Прямоугольным называется треугольник, если один из углов его равен 90 градусам, является прямым. Треугольник называется тупоугольным, если один из его углов больше 90 градусов, является тупым. Треугольник называется остроугольным, если все его углы меньше 90 градусов, все углы острые.
Равнобедренный треугольник Равносторонний треугольник

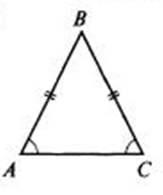
Для обозначения равенства сторон (когда стороны равны) вводятся специальные обозначения. Как на рисунке
Треугольник называется равнобедренным, если в треугольнике две стороны равны ( две равные стороны называются боковыми, а третья- основанием.
треугольник называется равносторонним, если у неготри стороны равны
- Высота. Медиана. Биссектриса треугольника
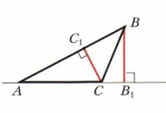
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противолежащую сторону
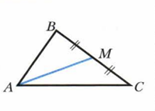
Медиана треугольника- отрезок, соединяющий вершину треугольника с серединой противолежащей стороны
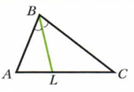
Биссектриса треугольника- луч, который делит угол пополам
Треугольники. Равнобедренный треугольник. Свойства и признаки

Равнобедренный треугольник — треугольник, у которого две стороны равны. Эти стороны называются боковыми. Третья сторона называется основанием. Вершина равнобедренного треугольника — вершина, соединяющая боковые стороны. Углы при основании — два других угла.
- Свойства равнобедренного треугольника
- Углы при основании равнобедренного треугольника равны
- Медиана, проведенная из вершины, является биссектрисой и высотой

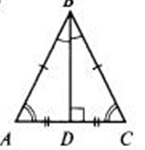
- Признаки равнобедренного треугольника
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
- Если медиана в треугольнике является биссектрисой и высотой, то этот треугольник равнобедренный. Или если высота треугольника является биссектрисой и медианой. Или. Если биссектриса треугольника является медианой и высотой

Треугольники. Признаки равенства треугольников
Два треугольника называются равными, если их можно совместить наложением. Если два треугольника равны, то равны все соответствующие элементы

Если два треугольника равны, то равны все соответствующие элементы
Признаки равенства треугольников — то есть необходимые признаки, по которым доказывается равенство треугольников. И это необходим для доказывательства равенства углов и сторон. Признаков равенства три. Итак подробнее.
- Первый признак равенства треугольников
Два треугольника равны, если у них равны две стороны и угол между ними. Если две стороны одного треугольника равны двум сторонам другого треугольника и углы, заключенные между этими сторонами тоже равны, то такие треугольники равны. и так равенство треугольников по этому признаку называется «равенство по двум сторонам и углу между ними». итак. Все подробности на чертеже..

2. Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.так этот признак называется «равенство по стороне и двум прилежащим к ней углам»

3. Третий признак равенства треугольников
Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны. Этот признак называется «равенство по трем сторонам»

Треугольники. Признаки подобия треугольников
Подобие и подобное встречается в нашей жизни довольно часто. Так. буквально, подобное — похожее — одинаковое по форме, но отличающееся по размерам. В геометрии тоже важно подобие. Но различающееся не просто, а пропорционально. Итак. Признаки подобия — условия. необходимые для доказательства подобия треугольников


Два треугольника называются подобными, если их углы соответственно равны, а сходственные стороны пропорциональны. Пропорциональными называют стороны, которые относятся с одинаоквым коэффициентом, называемым в дальнейшем коэффициентом подобия k ( коэффициент подобия равен отношению сходственных сторон. При этом площади подобных треугольников относятся с коэффициентом подобия в квадрате.



- Первый признак подобия треугольников
Если два угла одного треугольника равны двум углам второго треугольника, то такие треугольники подобны

- Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны

- Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
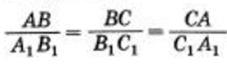
Треугольники. Средняя линия треугольника
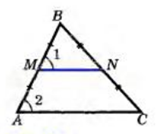
— линия, соединяющая средины сторон. Средняя линия параллельна третьей стороне и равна ее половине.
Для успехов в геометрии крайне важна хорошая база по математике. Итак. Без нее никак. Желаю успехов!!








