Функции — правила, с помощью которого значение (единственное) зависимой переменной находится по значению переменной независимой. Важно . каждому элементу множества X соответсвует единственное (!) значение множества Y. При этом функцию можно изучить по ее изображению. По графику.

Итак. Графики функций — это множество точек (x;y), удовлетворяющее условию y= f(x). Где x- независимая переменная, аргумент. y- переменная зависимая, значение ф-ции. По графику можно увидеть область опредения и область значения. Также можно найти нули ф-ции, можно видеть участки, где фукция убывает (возрастает). Легко видно промежутки знакопостоянства (участки, где функция имеет один и тот же знак). Например.

- Нули функций — значение аргумента, при котором значение ф-ции равно нулю.
- Промежуток знакопостоянства — промежуток, на котором функция принимает значения одного знака.
- Функция возрастающая

- Функция убывающия

Построение графика функции y= kf(x)
Построение графиков разбиралось ранее. Мы рассматривали на конкретных примерах, но здесь же попробуем обобщить. Итак, как коэффициент k влияет на график.

На рисунке хорошо видно, что, если k больше 1, то график «прижимается» к оси y/ Если k меньше 1, то график все больше «ложится» на ось x.

Теперь разберем как знак коэффициента k влияет на вид графика. Итак.

Итак. Обобщим. Как коэффициент влияет на график.

Построение графиков функций y= f(x) + b; y= f(x+a)
Легче всего понять на примере, так как хорошои видно на графике. Параллельный перенос графика. Или сдвиг по оси y. На 2. b=2.

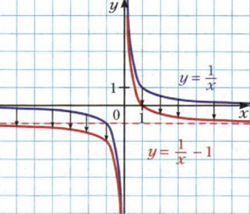
Свободный коэффициент перемещает график исходной (y= f(x)) по оси OY, на величину коэффициента b (y= f(x) + b) То есть, на примере
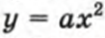

Это правило «работает» для всех функций. Например

Теперь рассмотрим построение графика y= f(x+a). И рассмотрим на примере все той же
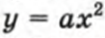
Теперь график смещается по оси OX. Например

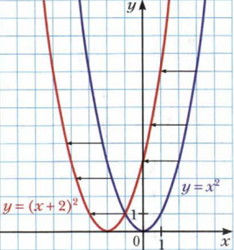
Используя график f(x), можно легко получить график f(x+a), смещая его по оси OX вправо. если a меньше нуля. и влево, если a больше нуля, на a единичных отрезков. То есть

Все параболы одинаковы, только расположены на координатной плоскости отлично друг от друга. Так можно строить любую функцию и менять ее расположение в зависимости от коэффициентов. Например


Все очень просто. Если есть шаблон f(x), то для построения f(x+3), например, как на рисунке, график f(x) смещаем по OX влево на три единичных отрезка, так как 3- число положительный, а значит, параллельный перенос на три влево. Как на рисунке слева.
И параллельно переносим вправо на 1, как на правом рисунке, так как функция f(x-1) получается смещением фукции f(x)
Рассмотрим функцию, в которой участвуют все возможные коэффициенты.
Построим график
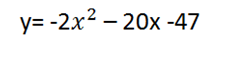
Для построения преобразуем функцию. Получим следующее превращение. f(x) ——— y= kf(x+a) + b

то есть из f(x) получили y= kf(x+a) + b, где

Алгоритм построения будет следующий:


Итак, график

Резюмируем. по такому алгоритму строится любая (почти любая) функция. Находим функцию «начальную» и смещаем ее. Согласно алгоритму и по всем преобразованиям. Это прекрасно.








