Окружность. Длина окружности.

Окружность. Это самое нелюбимое из курса геометрии. Особенно не «заходит» описанные и вписанные оружности. Но окружность — самое совершенное геометрическое чудо.

Недаром древние греки считали круг самой совершенной, «самой круглой» фигурой. И мы, между прочим, в жизни, часто употребляем это слово. всегда в значении «абсолютный». Круглый отличник, например. поэтому изучаем с особой тщательностью и любовью. На уроках математики практически нет практических занятий. Как на физике, например. Но это, конечно, не очень здорово. Поэтому прекрасно, что есть одно, но очень интересное мероприятие. Потому что целое большое научное открытие. Потому что всегда проходит на «ура». И всегда изумляет результат.

Из подручных средств. То есть категорически без циркуля Нам понадобятся: цилиндр, часто просто туба от туалетной бумаги и другие бытовые цилиндры. А также нить (для измерения длины окружности путем обматывания) и линейка). проводим эксперимент. И затем находим то самое. Грандиозное число Пи. Итак, начинается знакомство с кругом в средней школе. От простого к сложному. Потому что из эксперимента получается, что любой круг при делении длины окружности на диаметр дает одно и тоже значение.

Итак, после, практически сразу же, вводится базовая формула. «Все, что нужно знать об окружности»

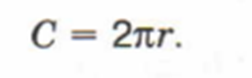
Здесь C- длина окружности, r- радиус (та самая равноудаленность от центра)

Окружность. Основные определения

Итак. Это геометрическое место точек, равноудаленных от данной точки (центр окружности).

Геометрическое место точек

множество всех точек, которые обладают определенным свойством

Хорда — отрезок,который соединяет две точки окружности. Диаметр — хорда, проходящая через центр окружности. Радиус— отрезок, который соединяето точку окружности и ее центр. На рисунке.

О -центр окружности

ОВ, ОХ, ОD, OB- радиусы

AB — хорда,

DB — диаметр

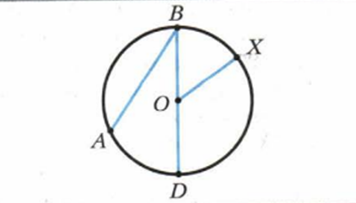
Круг -это геометрическое место точек, расстояние до которых от заданной точки (центра круга) не больше данного заданного числа (радиус круга).

Свойства окружности

Прежде, чем обсуждать свойства окружности. введем некоторые новые определения. часто в школьном курсе в теории изадачах фигурируют такие фигуранты, касательная к окружности, вписанные углы. центральные углы, дуги, а также касательная к окружности. Чтобы определиться с касательной, рассмотрим варианты взаимного расположения окружности и прямой. Очевидно, что прямая может не иметь общих точек с окружностью, а также две точки пересечения или одну. Но остановимся на последнем варианте. Это и есть касательная.

Касательная к окружности

Прямая. которая имеет только одну общую точку с окружностью

• Свойство касательной

касательная перпендикулярна радиусу, проведенному в точку касания.

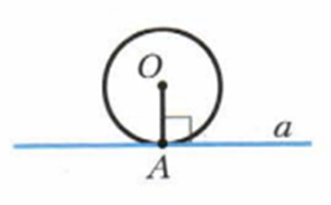
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

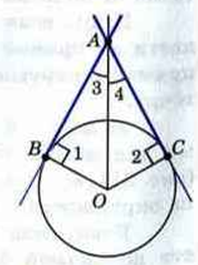
• Центральные и вписанные углы

Дуга окружности — часть окружности. заключенная между двумя точками. точки расположены на окружности. Полуокружность — дуга. ограниченная диаметром.

Центральный угол — угол, вершина которого лежит на окружности.

Вписанный угол — угол, вершина которого лежит на окружности.

Градусная мера дуги равна градусной мере центрального угла, который опирается на эту дугу.

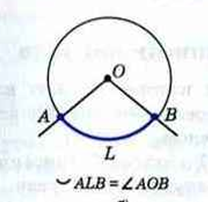
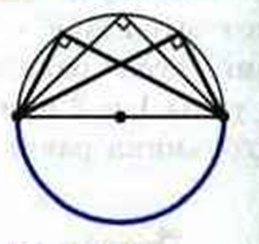
Вписанные углы, опирающиеся на одну и ту же дугу, — равны.

Вписанный угол, опирающийся на диаметр, равен 90 градусам

Окружность, описанная около четырехугольника

оружность описана около четырехугольника, если она проходит через все его вершины

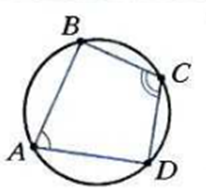
Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна 180 градусам.

Около любого треугольника можно описать окружность (об этом отдельно и подробно позже), но не всякий четырехугольник можно вписать в окружность. Итак. условия вписания.

Вписанный в окружность четырехугольник

Если в четырехугольнике сумма противолежащих углов равна 180, то около него можно описать окружность

Итак, параллелограмм никогда не впишется, а вот прямоугольник — всегда