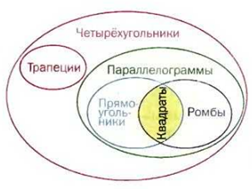
Четырехугольники — это отдельная группа в классе многоугольников.

Итак, многоугольник — фигура, состоящая из нескольких звеньев — сторон. Это фигура, образованная отрезками, то есть ломаная, концы которой замкнуты. Итак, рассмотрим на рисунке слева фигура ABCDEFG — ломаная, а фигура ABCDEFG справа — многоугольник.
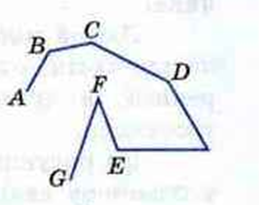
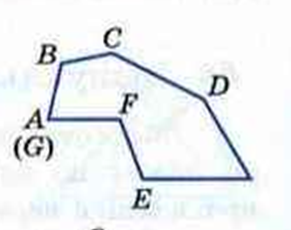
Итак. Многоугольник- фигура, замкнутая ломаная, если несмежные стороны не имеют общих точек. Ломаная, звенья которой — стороны многоугольника, а периметр- длина ломаной.
n- угольник
— это многоугольник с n вершинами. Он имеет n сторон, а также n сторон
Треугольник — n-угольник, у которого n= 3
Четырехугольники. Выпуклый многоугольник
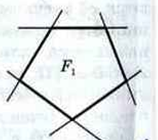
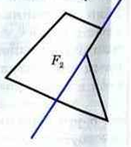
Многоугольник называется выпуклым, если он лежит по одну сторону от прямой, проходящей через две его вершины. Итак, на рисунке F1 — выпуклый, F2- нет
Итак, сумма углов выпуклого n-угольника равна
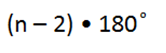
итак, подставляя n=4, получаем, что сумма внутренних углов четырехугольника равна 360 градусов. Но сумма внешних углов выпуклого многоугольника также равна 360. Итак, внешним углом многоугольника называется угол, смежный с углом многоугольника,при этом вычислить и доказать этот замечательный факт можно самостоятельно. Так как если при каждой вершине выпуклого многоугольника A1A2A3An взять по одному внешнему углу, то сумма этих внешних углов окажется равной 360 градусам.
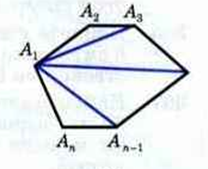
Действительно, если внешний угол равен 180 — A1, и так далее 180 — A2…., 180 — An,
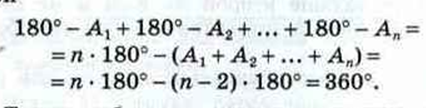
Итак, сумма внешних углов выпуклого многоугольника равна 360 градусов. Итак, всегда. И для любого многоугольника.
Четырехугольники
Четырехугольник — это n-угольник, у которого n=4. Итак, это многоугольник, у которого четыре вершины, четыре угла, четыре стороны, при этом стороны, исходящие из одной вершины, называются соседними, а стороны, не имеющие общего конца, называются противоположными. и еще, важно. четырехугольник обозначается буквами его вершин, а вершины перечисляются по порядку. Периметр четырехугольника- сумма длин его сторон. И важно. Если все вершины четырехугольника лежат на некоторой окружности. то такой четырехугольник называется вписанным. А если все его стороны касаются екоторой окружности, то называется описанным.
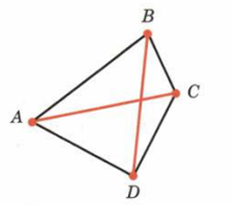
Итак, попробуем вычислить сумму углов четырехугольника. Так как каждая диагональ четырехугольника делит его на два треугольника, можно легко вычислить сумму углов четырехугольника. Итак, сумма всегда равна 360 градусов. Или еще проще, но по формуле.
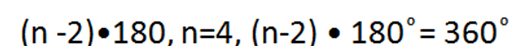
Четырехугольники. Параллелограмм
Параллелограмм
четырехугольник, у которого противолежащие стороны попарно параллельны.
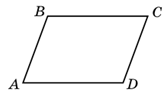
Свойства параллелограмма
- Противоположные стороны и углы равны.
- Диагонали параллелограмма точкой пересечения делятся пополам
- Сумма соседних углов равна 180 градусов
- Высота параллелограмма — это перпендикуляр, который проведен из любой точки стороны параллелограмма, к прямой, содержащей противолежащую сторону

Признаки параллелограмма

Четырехугольники. Прямоугольник
Прямоугольник
паралллелограмм, у которого все углы прямые
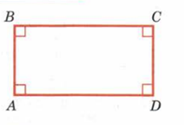
Свойства прямоугольника
- все свойства параллелограмма
- диагонали прямоугольника равны
- точка пересечения диагонали равноудалена от его вершин
Признаки прямоугольника

Четырехугольники. Ромб
Ромб
— это параллелограмм, у которого все стороны равны
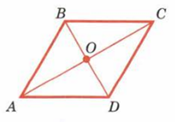
Свойства ромба
- все свойства параллелограмма
- диагонали перпендикулярны
- диагонали являются биссектрисами его углов
Признаки ромба

Квадрат
Квадрат
это прямоугольник, у которого все стороны равны, или ромб, у которого все углы равны, так как квадрат является и ромбом, и прямоугольником
Свойства квадрата
- все свойства прямоугольника
- диагонали квадрата перпендикулярны
- диагонали квадрата являются биссектирсами его углов
Признаки квадрата

Четырехугольники. Трапеция
Трапеция
четырехугольник, у которого две стороны параллельны, но две другие строго нет
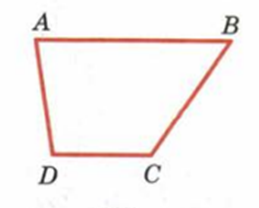
Так как трапеция — четырехугольник, у которого две стороны параллельны, а две другие строго не параллельны, легко догадаться, что параллельные стороны называются основаниями, а две другие — боковыми сторонами. Если боковые стороны равны, трапеция называется равнобокой. Если один из углов трапеции прямой, такая трапеция называется прямоугольной.
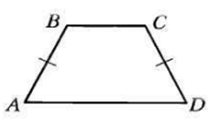
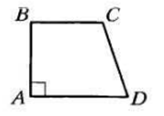
Свойства трапеции
- Сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусов
- трапеция является выпулым многоугольником
Свойства равнобокой трапеции
- углы при основании равны
- диагонали равны
- высота трапеции, проведенная из тупого угла. Итак, она делит основание на отрезки, при этом меньший из них равен полуразности оснований, а больший — полусумме оснований. (Это, кстати равно средней линии трапеции)

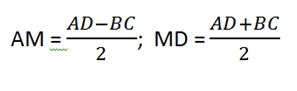
- средняя линия трапеции
Средняя линия трапеции
отрезок, соединящий середины боковых сторон
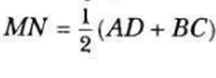
Средняя линия трапеции параллельна основания, а также легко вычисляется. Итак, средняя линия трапеции равна полусумме оснований.
Итак, обобщая все вышесказнное, рассмотрим рисунок, на котором хорошо видны все представители класса четырехугольников. При этом легко заметить, что трапеции — особенный класс ( или вид) четырехугольников.