Итак, отношения и пропорции — это то, что чаще всего занимает нашу жизнь. Итак, это самое важное во всех сферах человеческого бытия. Потому что отношения выстраиваем на работе, отошения строятся в семье, среди друзей и самыеилюбимые — среди любимых. попробуем разобраться в отношениях через отношения чисел. Итак, отношения в математике.

Отношения
- Определение
Как известно, в русском языке много синонимов. В математике тоже, не так часто, но встречаются. Итак, отношение — это частное двух чисел, это дробь.

- Отношения на примерах
Например. 16:4 — отношение 16 к 4. То есть, это отношение показывает во сколько раз 16 больше 4.
3:7 — отношение 3 к 7, поэтому показывает какую часть 3 составляет от 7
0,3: 0,11 — отношение 0,3 к 0,11.
При этом, форма записи может быть любая. То есть можно записывать в виде дроби, можно с помощю знака деления, потому что такая форма записи не очень удобна
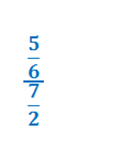
Итак, форма записи значения или сути не меняет, поэтому можно записывать так, как удобно.
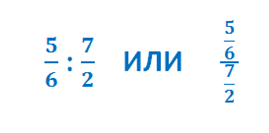
Например, дорожный знак «уклон дороги», Сопровождается числовым значением. На самом деле все просто, число показывает отношение высоты дороги к ее длине. Итак, проще, на пальцах, 12% кривизны- 100 м пути — 10 м высота.

Итак, проехав 100м по дороге с таким знаком, автомобиль поднимется на высоту 12 м.
Важно. Так как отношение — дробь по сути, можно по основному свойству дроби вывести основное правило отношений. Итак, если a и b натуральные числа, «работает» основное свойство дроби, а именно:
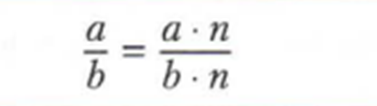
основное свойство дроби
- Свойство отношений

Основное свойство отношений хорошо работает для преобразований дробных выраений в дробь, так как отношение дробных чисел можно заменить оношением натуральных чисел. Например
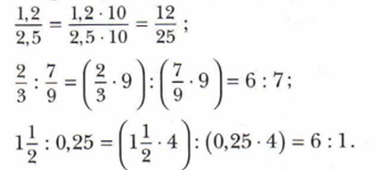
Итак, эти примеры иллюстрируют как отношение дробных чисел моно заменить отношением натуральных чисел.
Итак, резюмируя. Отношение — это- на примерах:

И, конечно, масштаб. Об этом чуть позже (чуть ниже).
Отношения и пропорции
Итак, рассмотрим следующее. 3,6:0,9 = 4 и 1,2 : 0,3 = 4,то есть можем записать следующее:
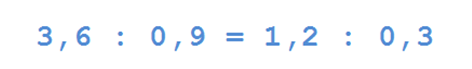
или так:

Или можно обобщить. В буквах
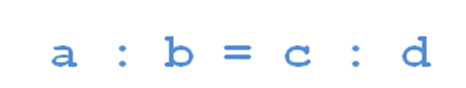
или так:
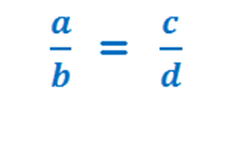
Отношение a к b равно отношению c к d. Или. a относится к b также, как c относится к d.
Итак. Пропорция.

пропорция
Важно.
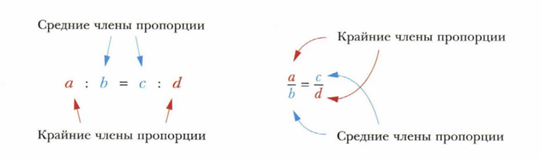
Еще важнее. В верной пропорции произведение крайних членов равно произведению средних. Итак.

То есть
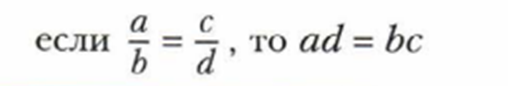
И обратно.

на примерах.

Процентное отношение двух чисел
Например. Каждый день мы пьем чай. Из одной и той же кружки. Размешиваем в ней одинаковое количество сахара. Стабильность — признак успеха. Но ничто не вечно под луной и чашка разбивается. Привычка остается. И вот мы пьем чай из другой чашки. Другая чашка = другой объем = другое количнство сахара. Стоп. Уже задачка. Как пить из другой чашки, не теряя сахарность. все верно, высчитываем новое количства сахара. Допустим, старая чашка -250 мг, новая — 400. Сахара было три ложки (30 гр), получаем
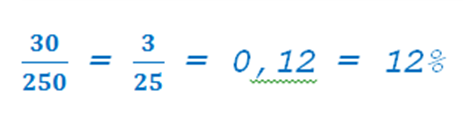
12% — «сахарность» чая, то есть какую часть составляет сахар от чая. И теперь легко рассчитаем количество сахара для новой чашки:
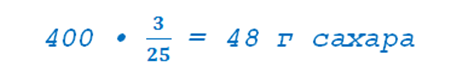
При этом 0,12- процентное соотношение массы сахара в чае. Очевидно, что
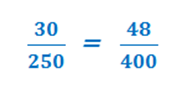
Или. Любимое. Самое понятное и близкое на уроках математики в 6 классе. Например. В классе учится 12 девочек и 20 мальчиков. Какой процент девочек в классе? Очевидно же:
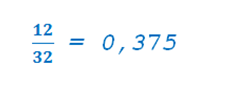
0,375 = 37,5 % — процентное «содержание» девочек в классе. Важно и полезно записывать это процентное соотношение в следующем виде:

можно также найти процентное отношение количество девочек к количеству мальчиков
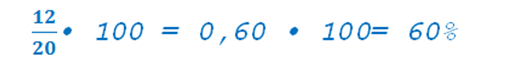
Такую форму записи можно и нужно тренировать для будущего. Для великого будущего в химии. Итак

Важно. Какую часть одно число составляет от другого, или какое процентное отношение одного числа от другого — есть суть одного и того же.
Итак.

Прямая и обратная пропорциональность
- Прямая пропорциональность
Разберемся с пропорциональностью. все мы так или иначе сталкиваемся с этим понятием и применяем его в жизни. Как правило, применяем правильно и интуитивно чувствем эту самую пропорциональность. Например. Если сторона квадрата увеличится в два раза, то и периметр квадрата увеличится в два раза. Легко покажем это:
P = 4a, a увеличивается в два раза и становится 2a. То есть новый периметр будет
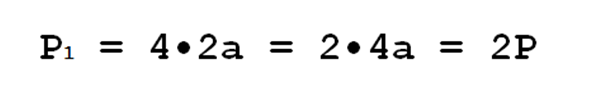
Увеличилась в два раза сторона- увеличился в два раза периметр. Периметр увеличился пропорционально стороне. Итак.
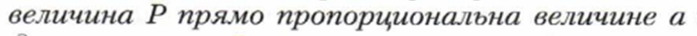
То есть

- Обратная пропорциональность

Рассмотрим опять геомтерическую задачу. Площадь. Площадь прямоугольника. Увеличиваем одну сторону в два раза. Чтобы площадь осталась прежней, вторую сторону нужно уменьшить тоже в два раза. Итак. S= ab. То есть теперь одна сторона увеличивается в два раза. а другую необходимо уменьшить в два раза. Итак, проверим
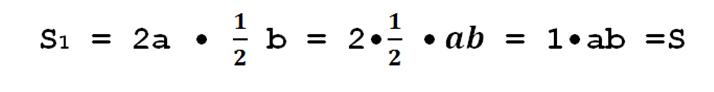
То есть стороны прямоугольника (в данной конкретной задаче!!) обратно пропрциональны.
Задачи на пропорциональность можно решать с помощью пропорций. Рассмотрим на примерах.

Итак, для начала нужно установить наличие пропорциональности между величинами. Очевидно, зависимость между величинами есть и она пропорциональна. Чем больше возьмем конфет, тем больше заплатим, то есть зависимость прямая. Пусть x — стоимость 1,5 кг товара. Тогда запишем условие задачи в правильном формате, чтобы видеть зависимость. а в дальнейшем увидеть нужную нам пропорцию

Здесь важно соблюдать порядок. Так обязательно следить, чтобы товар был в одном «столбце», а стоимость в другом.Вано также соблюдать единицы измерения. Они должны быть одинаковыми. И,если условие записано правильно, решение не составит труда, так как правильная запись условия и есть «готовая» пропорция:
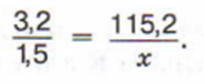
а решить эту пропорцию не составит труда, так как, зная основное правило пропорции. неизвестный член пропорции находится уже «на следующем шаге»

Важно заметить роль стрелочек в условии задачи. Они как раз и показывают, что пропорция в задаче прямая, так как стрелочки сонаправлены. Рассмотрим задачу, где стрелочки разнонаправлены. Это задача на обратную пропорциональность. Итак.

Похожая задача была разбрана выше, очевидно, здесь обратная пропорциональность, поэтому запишем правильно условие задачи. Здесь x — ширина второго прямоугольника.
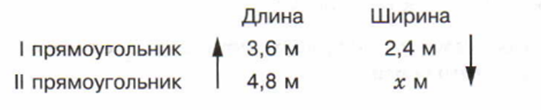
Очевидно, пропорция обратная, стрелки в разные стороны. Запишем пропорцию. Важно. Второе отношение «переворачиваем», так как пропорциональность обратная. То есть, если первую величину «мы» увеличиваем, то вторую необходимо уменьшить. Итак
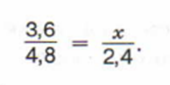
И решаем ее
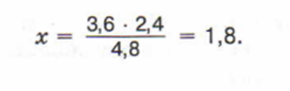
Масштаб
Участки земной поверхности изображают на бумаге в уменьшенном виде. При этом все пропорции соблюдаются. То есть мы имеем уменьшенную в несколько раз копию. Или макет. То, во сколько раз мы уменьшаем реальные размеры, и есть масштаб.
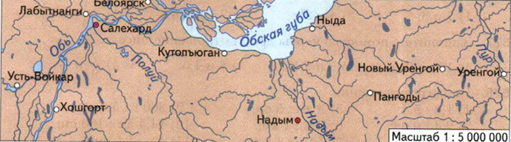
Зная масштаб, зная размеры на карте. можно легко вычислить размеры в реальности. Это обыкновенные задачи на пропорциональность. При чем пропорциональность всегда прямая. Рассмотрим на задаче.








