Уравнения — тема горячо любимая всеми без исключения. И, если это случилось(любовь), то это навсегда. Так, например, выбирая способ решения задачи, первое, что пробуется, — решение алгебраическое. Итак. Начнем с простейших, линейных. уравнений первой степени, далее сложнее и интереснее.

Простейшие уравнения
Уравнение — это равенство, содержащее одну или несколько нетзвестных. Неизвестные, как правило, обозначаются латинскими буквами, а именно, буквами x,y,z. Чтобы решить уравнение, найти корень уравнений, всегда надо найти те значения переменной (переменных), которые приводят уравнение в равенство. То есть при подстановке вместо тех самых переменных. Чему равен x — вечный вопрос и корень многих зол. Попробуем разобраться.

Простейшее уравнение — уравнение типа:

Уравнение, которые решается в одно действие и для решения требуются или простое заучивание правил:
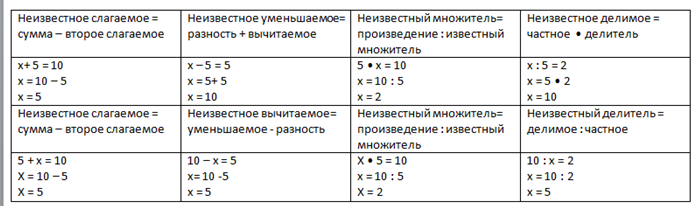
Или простая логика. Например. В уравнении x + 5 = 10 очевидно. неизвестное находится через вычитание. Или можно попробовать подобрать пример «на сложение» 2 + 3 = 5 «. «неизвестное слагаемое» 2 будет равно, очевидно же, 5 — 3. Никак иначе. Или придумывается история, желательно, чтобы увлекательно. У меня было сколько-то денег, мнем добавили 3 рубля и у меня стало 5 рублей. Сколько же у меня было? Проверено на людях. Когда заходит речь о денежных знаках, ошибки минимизируются. В данной задаче, конечно же, нужная сумма найдется легко и из следующего: 5-3. И так далее. Как и в любом деле, здесь нужна и крайне полезна практика. Опыт. Его величество опыт! Который, к счастью, приходит всегда и ко всем!
Простейшее уравнение — это уравнение типа:

Но! Если приобрести хорошую привычку и научиться решать уравнение «относительно скобки», то мы вернемся к началу и к нашим простейшим алгоритмам. То есть, например: уравнение (600 — x) — 92 = 126
Здесь неизвестный x «несвободен», так как он привязан к 600, поэтому будем считать, что неизвестное в этом уравнении — скобка- (600 — x), тогда все очевидно и просто. Итак, (600 — x) — неизвестное уменьшаемое.

, Легко заметить, что теперь получается действительно простейшее уравнение, которое решается легко. И просто.
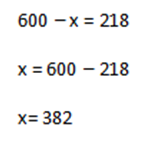
Итак уравнение «посложнее» решается также, как и простейшие, просто в два этапа, но важно следующее.

Любопытно. Занимательно. Важно. Применяем. Грамотность — наше все.
Уравнения линейные
Линейное уравнение с одним неизвестным x
Уравнение, у которого левая и правая часть — многочлены первой степени.
Итак. прежде, чем решать, необходимо вспомнить основные понятия, а также базовые приемы в алгебре.


Так как всегда линейное уравнение сводится к виду kx + b = 0, которое очень легко решается:

Находить корни не составит труда, так как для решения используется простой и понятный алгоритм. Итак, алгоритм нахождения корней. Всего два правила. Итак:

Чтобы лучше понять эти правила и поверить, что этого достаточно, чтобы решить любое линейное уравнение, рассмотрим примеры.

Все очень просто. Но ингода встречаются нетипичные ситуации, для примера рассмотрим следующее:
2x +5 = 2(x +6)
Раскроем скобки: 2x +5 = 2x + 12
Перенесем: 2x — 2x = 12 — 5
Приводим подобные слагаемые: 0x = 7, данное уравнение нерешаемо, то есть корней нет.
Решение задач алгебраически
Решение задач алгебраически — самый универсальный способ рашения задач вообще. Если понять и принять его один раз, разлюбить или перестать понимать будет уже невозможно. Решение задач с помощью уравнений всегда начинается со слов » пусть x», а далее начинается самое творческое в этом бесконечно творческом процессе. Или же, если рассматривать с точки зрения сложности в решении задач. Приняв какое — то неизвестное за x, далее нужно просто все условия задачи «перевести» на язык математический (алгебраический). Чтобы понять какие именно задачи можно и лучше решать с помощью уравнений? Это, как правило, задачи, где или больше неизвестных, связанных какими — то условиями меду собой. Вообще, здесь более чем в других областях все решает опыт и объем. Итак. Рассмотрим типичне задачи.









