Тригонометрия

Тригонометрия — раздел математики, изучающий тригонометрические функции или зависимости между углами и сторонами в треугольнике.

Решение прямоугольных треугольников

Ура! Самое популярное в геометрии, то есть самое простое, доступное, самое -самое любимое. Можно совсем не понимать, категорически не любить геометрию, в частности, или математику вообще, но! Теорему Пифагора — это навсегда! Это нельзя не понять.

Решить прямоугольный треугольник — значит найти все неизвестные стороны и неизвестные углы, то есть решить прямоугольный треугольник — значит найти все его углы и все его стороны. Итак, прямоугольный треугольник

Здесь CD- высота, опущенная на гипотенузу. AB — гипотенуза, AC и CB — катеты. Важно- AD и DB — проеции катетов на гипотенузу. Итак

Очень полезные формулы:

Но, самое главное, из этих формул легко получаем великую и любимую теорему Пифагора. Итак

Или в более привычном, то есть в универсальном виде:

Итак. теперь можно найти недостающую сторону по двум другим, так можно вывести формулы для поиска двух других сторон (или катетов):

Итак, зная две стороны в прямоугольном треугольнике, легко находим третью.

Тригонометрия. Метрические соотношения в прямоугольном треугольнике

Рассмотрим прямоугольний треугольник ABC, здесь угол C — прямой, сторона AC — сторона, противолежащая углу B, BC — углу A.

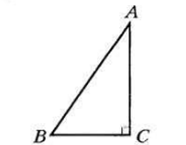
Итак, теперь основополагающие определения.

Синус острого угла

прямоугольного треугольника — это отношение противолежащего катета к гипотенузе.

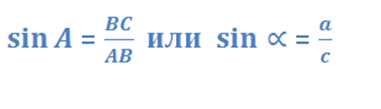
Косинус острого угла

прямоугольного треугольника — это отношение прилежащего катета к гипотенузе

Тангенс острого угла

прямоугольного треугольника — это отношение противолежащего катета к прилежащему

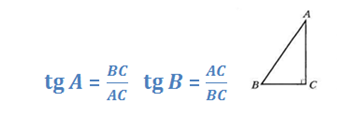
Тригонометрические функции

Итак, косинус, синус, тангенс, котангенс зависят от величины угла. То есть каждому острому углу соответствует единственное значение, соответсвующее значению синуса (косинуса, тангенса и котангенса), поэтому зависимость функциональная. Итак, функция, соответствующая этой зависимости, — тригонометрическая.

Тригонометрические функции

функциональныя завсимости, соответствующие значениям синуса, косинуса и тангенса, аргументами которых являются острые углы.

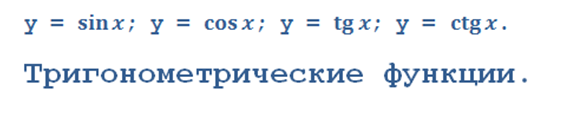
А теперь основное тригонометрическое тождество. Легко выводится, легко применяется и очень полезно.

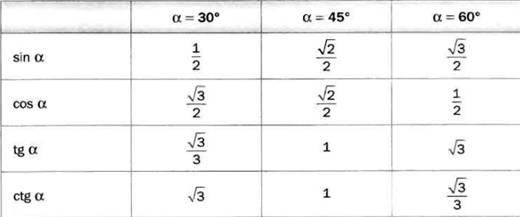
Некоторые значения некоторых углов

Формулы приведения

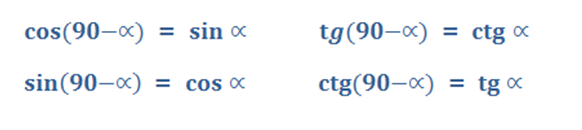
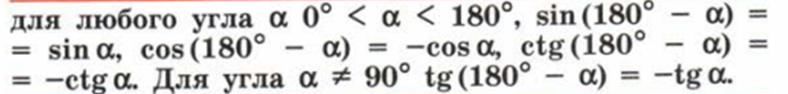
И еще одна прекрасная формула. Так как

Итак, получаем еще одну тригонометрическую формулу

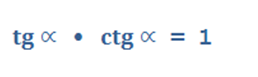
Тригонометрия. Теорема синусов

Итак, еще формула. следствие теоремы синусов:

Теорема косинусов

Чтобы найти неизвестную сторону стреугольника по двум известным и углу между ними.

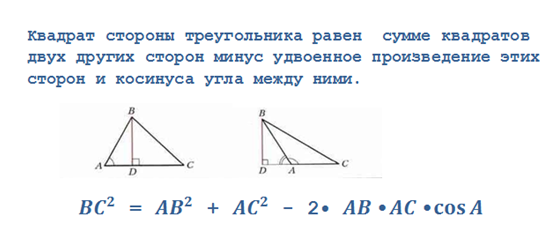
Итак, теперь рассмотрим прямоугольный треугольник, пусть угол A равен 90 градусам. Итак

Но где еще можно использовать теорему косинусов?

Чтобы опеределить тип треугольника.

Решение треугольников

Итак, решить треугольник — значит найти все его углы и все стороны. Для решения этой задачи как правило хватает теоремсинусов и теоремы косинусов.