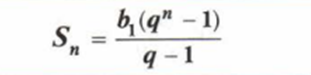Последовательности- любой пронумерованный набор обьектов. При этом последовательность может быть конечной, а может быть бесконечной. Как понятно из названия, в бесконечной последовательности бесконечное число членов, а в конечной — конечное. Итак

Числовые последовательности
Итак. Объекты, пронумерованные натуральными числами, образуют последовательность. Объекты назывются членами последовательности и каждый член имеет свой номер.

Числовая последовательность — это последовательность, которая состоит из чисел, при этом закономерность или правило составления последовательности бывают разные. Для обозначения используются буквы с индексами:

где индекс указвает на место в последовательности. последовательность можно задать словами, т.е. описательно, или с помощью формулы, например:
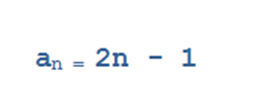
Итак, это последовательность нечетных чисел. Например:

Итак, здесь последовательности заданы с помощью формул. Можно создать последовательность задать с помощью описания, а также с помощью рекурентным способом.
Рекурентный способ
это способ задания, при котором последовательность с помощью начальных условий и рекурентной формулы.
Начальные условия
условия,которые определяют первый или несколько первых членов
Рекурентная формула
формула, определяющая член последовательности через один или несколько предыдущих членов
При рекурентном способе задания первый или несколько первых заданы. остальные вычисляются друг за другом.
Арифметическая прогрессия
В арифметической прогрессии каждый следующий член получается прибавлением одного и того же числа к предыдущему, итак

Итак, арифметическая последовательность.

Например: 1; 4; 7; 10;……… арифметическая прогрессия, в которой каждый последующий член больше предыдущего на три. То есть разность арифметической прогрессии d= 3, Так можно вычислить любой член прогресси по формуле,
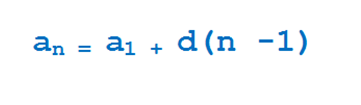
где a — члены прогрессии, d — разность арифметической прогресси. Здесь d = 3. Можно арифметическую прогрессию задать рекурентным способом, но для этого нужно к предыдущему члену прогрессии прибавить разность арифметической прогрессии.
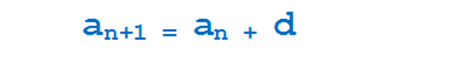
Из формулы видно, что каждый следующий получается из предыдущего увеличением на разность арифметической прогрессии, поэтому нетрудно догадаться, что каждый член в итоге получается из первого через многократное прибавление d, поэтому универсальной формулой арифметической прогресси будет формула следующая:

Любопытно, но каждый член арифметической прогрессии равен среднему арифметическому предыдущего и последующих членов
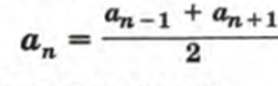
Итак, наконец, формула суммы первых n членов арифметической прогрессии:

Геометрическая последовательность
Рассмотрим порследовательность: 1; 3; 9; 27; ….. если внимательно посмотреть, можно заметить, что каждый следующий член последовательности умножается на три. Это самая популярная последовательность, которую активно используют в биологии при решении задач, итак

При этом число, на которое умножается каждый следующий член, называется знаменателем геометрической прогрессии.
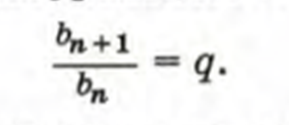
И, чтобы задать прорессию рекурентно, надо только знать знаменатель прогрессии и первый член, все последующие члены находятся через поступательное умножение.
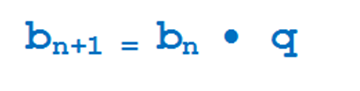
где q- знаменатель геометрической прогресси, b- члены прогрессии. Но также, как и в арифметической прогрессии, здесь удобнее пользоваться формулой n-го члена:

где q — знаменатель геометрической прогрессии, b — первый и n-й член прогрессии.
Любопытно и нетрудно заметить, что квадрат любого члена прогрессии равен произведению двух соседних членов, но не для первого члена, конечно же.
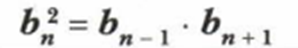
То есть, каждый член прогрессии есть среднее геометрическое двух соседних членов. Здесь bn+1 и bn-1 — члены предыдущий и последующий члена bn. Если члены последовательности положительны, то можно записать так:
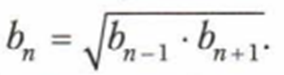
и сумма n- членов прогрессии: