
Отрицательные числа в школьном курсе математики появляются тогда, когда чисел обыкновенных уже не хватает, не хватает уже и чисел дробных. Очевидно, с отрицательными числами мы сталкиваемся рано и пользуемся всегда и легко, с ранних лет или даже раньше. Наши любимые градусники. Без них никуда, особенно в зимнее время. На них -то и объяснимся в теме отрицательных чисел. Итак.
Координаты на прямой
Знакомство с координатами начинается с координатного луча

Здесь вводятся координаты точки. Например. E(1)- точка E с координатой 1, N(3) — точка N с коородинатой 3 и так далее. Далее мы понимаем, что координат и, собственно точек, бесконечное количество, так как координатный луч — луч и не имеет конца. А теперь для полноты картины мы вводим координатную прямую

К координатной прямой неплохо возвращаться каждый раз, когда возникают вопросы при слоении. например. Но об этом чуть ниже.
Координатная прямая
прямая с выбранной точкой отсчета, единичным отрезком и направлением. Число, показывающее место точки на прямой, называется координатой точки. Обозначается координата определнным образом. Например, А(3) — точка А с координатой 3
Итак, координаты точек, находящиеся правее нуля имеют положительный знак, левее — отрицательный знак. И так числа бывают положительными и орицательными. В быту мы часто употребляем: «сегодня минус пять», например. Причем так и складываем легко числа с разными знаками, потому что, если температура «падает» от 2 градусов на 10 градусов, например, и получаем «минус восемь». Но на уроке пример «2-10» может вызвать трудность. Все дело в контексте?
Итак. Числа со знаком «минус» называются отрицательными. Конечно же, числа бывают целые, но бывают и дробными. Рассмотрим на примере.

Кроме градусника отрицательные числа используются и в других областях. например.

Противоположные числа
Понятно из названия, противоположные числа — числа, одинаковые по значению, но разные по знаку. Например числа «семь» и «минус семь» — числа противоположные. (7 и -7).

Противоположные числа
Два числа, отличающиеся только знаками
Целые числа
натуральные числа числа, противоположные им числа и нуль
Модуль числа
Противоположные числа находятся на одинаковом расстоянии от нуля, то есть расстояние от нуля (начала отсчета) до, например, точки А(4) и А(-4) одинаковое и равно четырем. Это расстояние и есть модуль числа.

Точка B(5) находтся на 5 единичных отрезков от О (начала отсчета). Можно сказать, что модуль числа 5 равен 5
Точка М(-6) находтся на 6 единичных отрезков от О(начала отсчета). То есть

Модуль числа не может быть отрицательным. Если число положительное, то модуль числа равен самому числу. Если число отрицательное, модуль отрицательного числа равен числу противоположному. И противоположные числа имеют равные модули
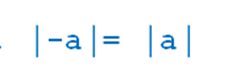

Сложение и вычитание чисел с разными знаками
Чтобы складывать любые числа ( с любыми знаками), необходимо понять и принять базовый приницп сложения:

Это все, что нужно знать для сложения чисел с разными знаками. Еще обязательно( или необязательно) нужна координатная прямая. В помощь. Например.
-7 + 4 = Точка А( -7) перемещается вправо на 4 единицы (изменение положительное- перемещение вправо), а значит попадаем в точку B с координатой 3. То есть

То есть получаем «минус три». Если хорошо потренироваться, прямая не понадобится совсем, но прежде. чем с ней «прощаться», нужно уяснить еще один момент. Если пользоваться координатной прямой для сравнения чисел, важно. Чем правее, тем больше. Больше то, что правее. Это очень помогает ориентироваться в области отрицательных чисел, где ориентироваться непривычно. Так как -7 меньше, чем -3, например. Итак:

И, например, » вычитание». -2 — 4 = — 6. Точка А(-2) перемещается влево (так как вычитаем ) на 4 единичных отрезка и попадаем в точку С( — 6).

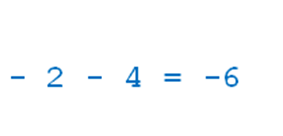
И важно.

Например. 4 + ( — 4) = 0

Так, используя координатную прямую, можно решать примеры любой сложности.
Сложение отрицательных чисел: -6 — 3 = — 9

Умножение и деление чисел с разными знаками
Здесь речь только о знаке результата. Числа умножаются по правилам умножения (и деления чисел. Дроби умножаются по правилам умножения дробей, натуральные числа — как натуральные числа)


Чтобы определить знак произведения, нужно посчитать количество отрицательных чисел, если множителей с » минусом» нечетно — результат отрицательный. Еще раз про любовь. Произведение двух чисел с разными знаками отрицательно, произведение двух чисел с одинаковыми знаками — положительно. Все!
Рациональные числа
Любое число можно представить в виде доби со знаменателем 1, поэтому любое число -рациональное. То есть

Итак, получается,любое рациональное число можно представить в виде десятичной дроби. Но при этом можно обнаружить дроби бесконенчые, а среди последних — дроби периодические. Вспомним:

Деление в этом случае бесконечно, видно хорошо на рисунке. Есть специальная форма записи для периодических дробей:








