Площадь — тема горячо любимая и понятная всем. Полезная в быту и алгоритимически простая. Есть формулы для базовых фигур, а также рекомендации для фигур нестандартных. В общем, хорошая тема.

Площадь многоугольников
Многоугольник — фигура уже известная, которую более подробно уже разбирали в предыдущих главах. Поэтому здесь сразу перейдем к поиску площади. Как известно, многоугольник — фигура неточная и многоугольников может быть огромное количество. Многоугольников разных и непохожих друг на друга. Одной общей формулы для поиса нет. но есть несколько базовых правил, а именно:
- равные многоугольнки имеют равные площади
- если многоугольник составлен из нескольких многоугольников, то площадь многоугольника равна сумме площадей этих многоугольников
- за единицу измерения площади принимают единичный квадрат, поэтому для нахождения площади нужно умножить на количество этих квадратов. Так часто на практике предлагают найти площади фигур на клетчатой бумаге (кстати, отдельный номер в ОГЭ по математике)
- для поиска площадей многоугольников, его разбивают на понятные фигуры, то есть на фигуры. площади которых можно легко найти. Тоже, кстати, любимое задание из ВПР, РДР и других страшных работ по математике.
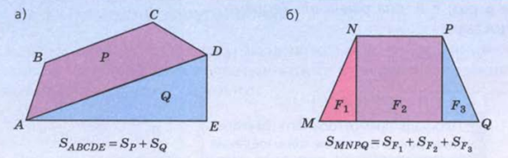
Итак. Основные свойства площади
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Равновеликие многоугольники
это многоугольники, у которых равные площади
Две прекрасные задачи на тему, которые любимы всеми авторами, интересные и красивые. Итак.

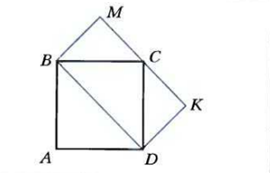
В задаче №1 требуется доказать равенство фигур ABCD и AKD
В задаче №2 требуется доказать равенство фигур ABCD и BMKD
И еще, важно, площади подобных фигур. итак

Подобие фигур обсуждалось и разбиралось выше.
Площади прямоугольников
Прямоугольник — фигура до боли известная всем, самая первая и самая базовая фигура. Изучается уже в детском саду, поэтому сразу перейдем к формуле. Итак.
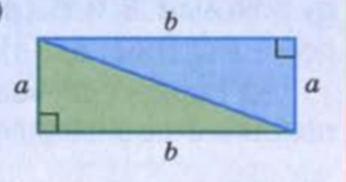
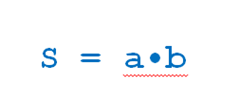
где a и b — смежные стороны.
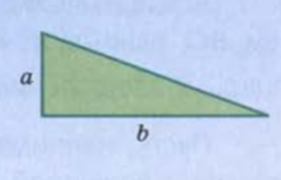
Здесь уместно перейти к формуле для нахождения площади прямоугольного треугольника, так как известно, что диагональ делит его на два равных треугольника, поэтому формула площади прямоугольного треугольника
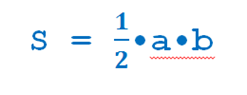
где a и b — катеты.
Также известная фигура — квадрат, тоже изучается » с пеленок». много раз повторяется, в начальной школе. в пятом классе точно, при прохождении темы «степень«. итак, формула для нахождения площади квадрата:
где a — сторона квадрата, как известно, в квадрате все стороны равны, так как квадрат — прямоугольник, у которого все стороны равны. Зная что такое степень, запишем новую версию, итак:

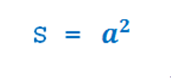
Площади треугольников
Про треугольник подробно здесь. Для пользы дела, условимся, что в треугольнике есть основание и высота к основанию. Итак
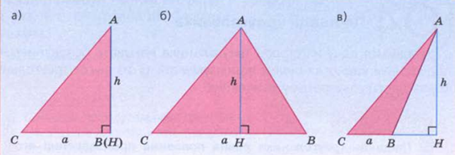
Треугольники бывают разные, высоты и основания тоже, но принципиально все треугольники по трем типам имееют одну и ту же «картинку», как на рисунке выше. Для поиска площади нам понадобится значение высоты и основания, но условно, в треугольнике возможны три варианта таких комбинаций, поэтому рекомендуется взять и назвать так ту, которая удобнее. Итак. Для нахождения площади треугольника нужно воспользоваться формулой:

где a — основание, h— высота к этому основанию.
Причем, как видно из рисунка, эта формула «работает» для любого типа треугольника, в том числе и прямоугольного, где высота совпадает с одним из катетов и «звучит» формула немного иначе:
Площадь прямоугольного треугольника
равна половине произведения катетов
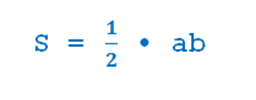
где a и b — катеты.
Есть еще две замечательные формулы:


Как » поется» в одной прекрасной песне: » все формулы хороши, выбирай на вкус».
Площадь параллелограмма
Так как параллелограмм — четырехугольник, у которого стороны попарно параллельны и равны, договримся, что одну сторону назовем основанием, а перпендикуляр, проведенный к ней — высотой.
Так на рисунке AD — основание, BH — высота к этому основанию
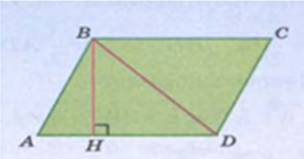
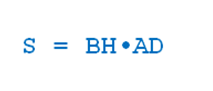
Для нахождения площади параллелограмма, надо основание умножить на высоту.
Площади трапеций
Трапеция — фигура, которую разбирали ранее, поэтому перейдем сразу к формуле. Высотой трапеции называют перпендикуляр. проведенный из любой точки одного основания к прямой, содержащей другое основание.
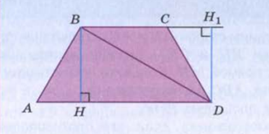
Для нахождения площади трапеции нужно умножить высоту на полусумму оснований.
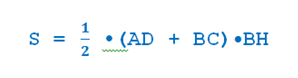
Или, иначе:
Для нахождения площади трапеции
нужно среднюю линию трапеции умножить на высоту
Площади четырехугольников
Здесь же уместно привести формулу для вычисления площади четырехугольника
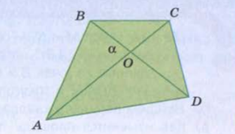

Формула Герона









