Неравенства, оакзывается, тоже решают. И решают, оказывается, по всем правилам. И несмотря на кажущуюся нестройность и нестрогость, решается все строго по инструкции. Итак

Числовые неравенствa
Прежде чем решать неравенствa, определимся с понятиями. Что такое неравенство. Оригинально, но неравенство — это результат или путь к результату для сравнения. Часто сравнивая что — либо, мы резюмируем, что да, это больше другого. Так, сравнивая числа между собой, мы заключаем. что 2 больше 1, что деясть больше девяти. Мы легко разбираемся в области отрицательных чисел, хоть там и все наоборот. Так, -2 больше -3, так как мы знаем «золотое» правило сравнения, а именно: что правее (на координатной прямой), то и больше. Прекрасное правило. Никогда не подводит.

Это правило применяется и для алгебраических выражений. Рассмотрим на примере. Решим неравенство

Перенесем влево правую часть и посмотрим что получится. Преобразуем алгебраическое выражение в левой части.

При любом a разность отрицательна. поэтому равенство верно.

Итак, чтобы показать, что одно больше другого, надо вычесть и посмотреть на знак разности, если разность меньше нуля, уменьшаемое меньше вычитаемого. Конечно же, это не все, что можно и нужно знать о решении неравенств. Поэтому рассмотрим неоторые свойства неравенств.
Если c — положительное число, то точка с координатой b + c лежит правее точки b, если c — отрицательна, то левее.

И, что очень важно, поэтому повторим. Если a больше b, точка с координатой a лежит правее точки с координатой b, а если b больше a, то a лежит левее точки с координатой b. Итак, свойства числовых неравенств.
Неравенствa. Некоторые свойства числовых неравенств
Здесь рассмотрим основные свойства числовых неравенств. Итак, правило один.

Правило два.

Или другими словами, мы можем прибавлять к левой и правой части одинаковые слагаемые. Неравенство при этом останется прежним. Все так, как и в уравнениях. Итак

Или, тоже, как и в уравнениях,

Правило три.

Аналогично, если a меньше b и с- положительное, то ac меньше bc и наоборот, если a меньше b и c отрицательное, то ac больше bc. То есть

Другими словами, чтобы решить неравенство, можно также, как и уравнения, умножать и делить, но есть нюансы. Итак,

И еще одно свойство числовых неравенств:

Неравенства. Решение линейных неравенств с одной переменной
Чтобы решить неравенство, используют правила, рассмотренные чуть выше. Алгоритм решения тоже похож на решение уравнений. То есть, преобразуем неравенство и приводим к виду ax + b > 0 или ax + b < 0, которое решается аналогично уравнениям вида ax + b = 0 Теперь добавим несколько свойств.
Сложение неравенств.
При почленном сложении верных неравенств одного знака, результатм является верное неравенство того же знака. При этом одним знаком неравенств называют следующее:

итак, сложение неравенств одного знака.

Если сложить почленно неравенствa одного знака, то получится верное неравенство.
Умножение неравенств одного знака.

Если почленно перемножить верные неравенствa одного знака, левые и правые части которых – положительные числа, то получится верное неравенство.
СЛЕДСТВИЕ.
Если a и b положительны и a < b, то < , где n – натуральное число.
Чтобы решить неравенство, надо, пользуясь всеми правилами, найти значение переменной, которое обращает неравенство в верное числовое неравенство.

Неравенствa. Решение неравенств второй степени с одной переменной
Неравенствами второй степени называют неравенствa вида

где x — переменная, a, b, c — числовые коэффициенты. Решением будут промежутки, гле фукция принимает положительные или отрицательные значения. Чтобы это определить, достаточно проанализировать как ведет себя функция, то есть рассмотреть как будет расположен график в системе координат, а именно: куда направлены ветви, есть ли нули функции и т.д.
Рассмотрим на примере. Решим неравенство:

Графиком функции y=5x2+ 9x — 2 является парабола, ветви которой расположены вверх. Найдем нули функции, для чего решим уравнение:

Уравнение имеет два корня:

парабола пересекает ось x в двух точках. Так как ветви расположены вверх, промежуток, где функция отрицательна, хорошо считывается, а именно: это промежуток
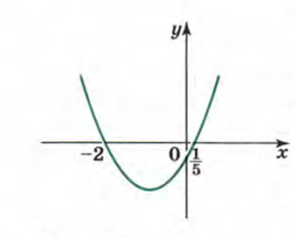
решением неравенствa 5x2+ 9x — 2 < 0 является числовой промежуток:
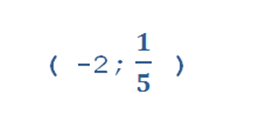
Аналогично решаются аналогичные неравенствa второй степени. Есть алгоритм решения такого рода неравенств

Неравенства. Решение неравенств методом интервалов
Пусть функция задана формулой

где x — переменная, а x1, x2….. xn — нули функции. И на каждом промежутке между нулями функция знак сохраняет, а при переходе через нуль, знак меняет. Это и есть ключ для решения неравенств. Рассмотрим следующее

получаем промежутки. Чтобы определить знак на промежутке, нужно задать какую — нибудь точку на этом промежутке. Какой знак получится у функции. такой будет знак у всего промежутка. останется только чередовать промежутки и знаки и сделать правильную выборку. Как обычно. рассмотрим на примере.
Решим неравенство: — x( x – 0,5 )( x + 4)< 0, для этого совершим все необходимые преобразования.

Нетрудно заметить, ответом будут следующие промежутки:









