Все теоремы, конечно, невозможно, но основные и чаще других используемые в школе, — легко. Так, например, теорма Пифагора, любимая и до боли знакомая.

Все теоремы в одном месте, потому что мы хотим знать, любить и понимать геометрию. Потому что удобно,когда все под рукой.



Итак, прежде, чем разбирать теоремы, необходимо определиться с понятиями. Преждем, чем изучать или разбирать теорему Пифагора, нужно вспомнить определение прямоугольных треугольников, а также их свойства. Итак, начинается все с определений.
Все теоремы геометрии. Определения.



Угол называется смежным, если если у них одна сторона общая, а две другие вместе образуют развернутый угол. Угол называется вертикальным, если образован двумя пересекающимимся прямыми. И важно, что смежные, так и вертикальные, углы всегда представлены парой. Если идет речь о вертикальных или смежных углах, то всегда говорят во множественном числе.

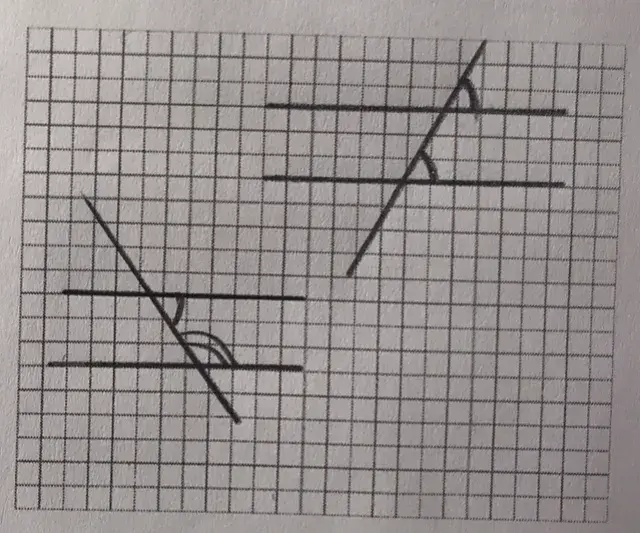

Углы накрест лежащие, а также соотвественные и односторонние всегда получаются при пересечении двух прямых третьей прямой. Две, как правило, являются параллельными, а третья всегда называется секущей. Далее рассмотрим признаки параллельности прямых, потому что представленные выше углы играют решающую роль. Важно запомнить визуально какие пары углов как называются, так как названия при этом выбраны неслучайно.



Центральный угол — угол, вершина которого лежит в центре окружности. Лучи пересекают эту окружность. Вписанный угол — угол, вершина которого лежит на окружности. Стороны при этом пересекают ее.

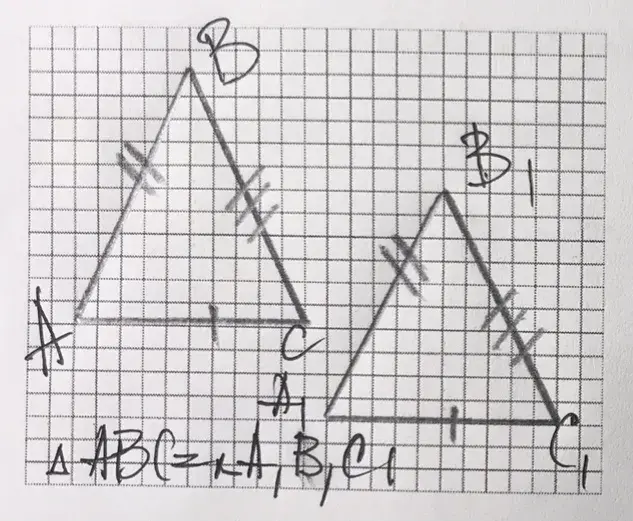

Треугольники называются равными, если все их соответсвующие элементы равны. То есть равны углы и равны стороны.Треугольники называются подобными, если углы треугольников равны, а стороны пропорциональны. Итак, пропорциональность сторон определяет коэффициент подобия k.



Равнобедренным треугольником называется треугольник, если две стороны его равны, При этом третья сторона называется основанием. А две другие — боковыми.

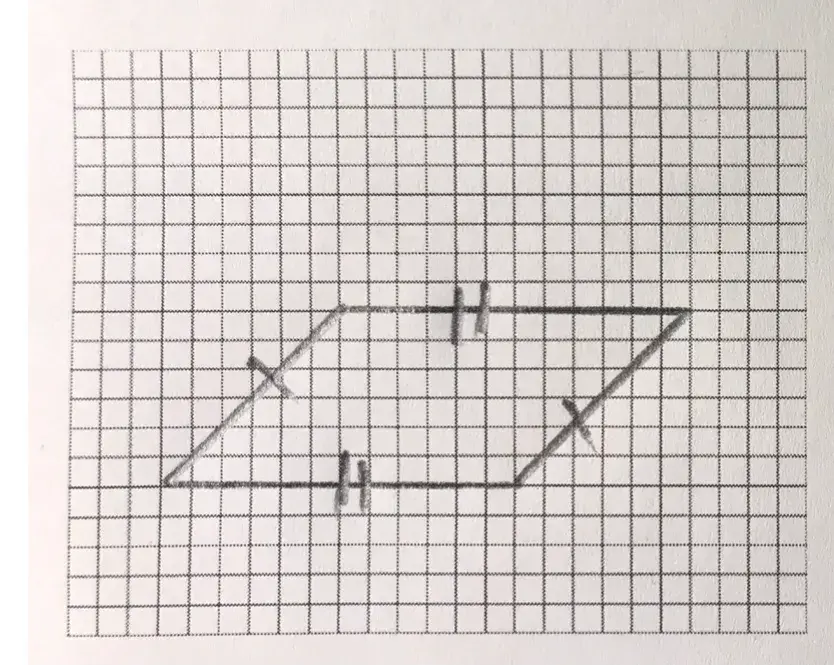

Параллелограмм — четырехугольник, у которого стороны попарно параллельны. Прямоугольник — параллелограмм, у которого все углы прямые.



Квадрат — прямоугольник, у которого все стороны равны. Ромб — параллелограмм, у которого стороны равны.



Если две стороны четырехугольника параллельны, этот четырехугольник — трапеция. Бывают равнобокие трапеции и трапеции прямоугольные. Тема важная, так как систематизирует и собирает в одном месте все самое важное. Тема, без которой невозможно решать задачи по геометри, поэтому невозможно успешно сдать свой любимый экзамен ОГЭ . Поэтому заслуживает отдельной главы. Итак, глава «Все теоремы геометрии». Встретимся там.








